Предмет: Геометрия,
автор: frog2491
Боковое ребро правильной четырехугольной усеченной пирамиды образует с диагональю большего основания угол в 45°. Найдите длину диагонали усеченной пирамиды, если стороны ее оснований равны 24 см и 7 см.
siestarjoki:
25
Ответы
Автор ответа:
2
Продлим боковые стороны до полной пирамиды.
Диагональ большего основания AC=AB√2 (диагональ квадрата)
∠SAC=∠SCA=45°, △ASC - равнобедренный прямоугольный
SA=AC/√2 =AB
Боковые грани полной пирамиды - равносторонние треугольники.
Проведем EC1||BB1.
△EC1C подобен △BSC и также равносторонний, EC=CC1
∠ACE=45° (диагональ квадрата является биссектрисой) =∠ACC1
△ACE=△ACC1 (по двум сторонам и углу между ними) => AE=AC1
BE=B1C1 =7 (параллелограмм)
Из △ABE по т Пифагора AE=25
AC1=AE=25 (см)
Приложения:
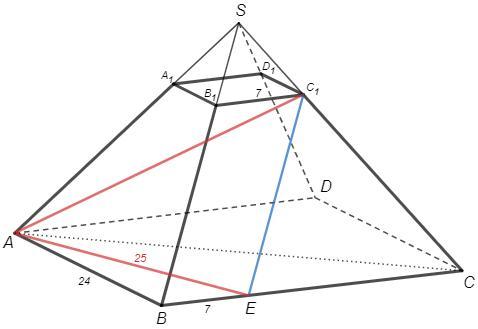
Разумеется, можно просто рассмотреть трапецию AA1C1C. Равнобедренная с углами 45, основания 7√2 и 24√2.
Похожие вопросы
Предмет: Русский язык,
автор: КсюшаFA
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: LipGallagher69
Предмет: Химия,
автор: annakrechko04