Помогите с геомой!
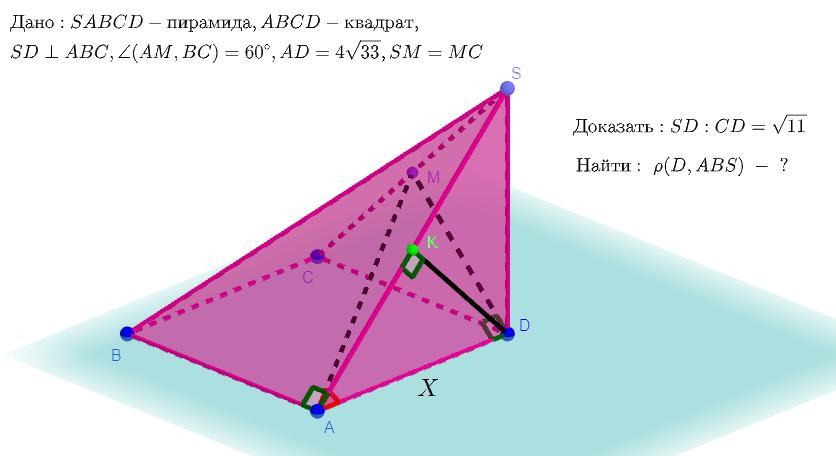
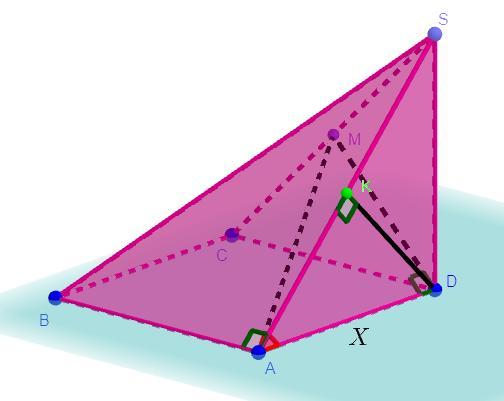
Основанием пирамиды SABCD является квадрат ABCD. Высота пирамиды проходит через точку D; M-середина ребра SC; Угол между прямыми AM и BC равен 60 градусов.
a) Докажите что SD:CD = корень из 11
б) Найдите расстояние до точки D до плоскости ABS, если сторона остования пирамиды равна 4 корней из 33. С РИСУНКОМ
Ответы
Ответ:
Объяснение:
Дано: SABCD - пирамида, ABCD - квадрат , SD ⊥ ABC, ∠(AM,BC) = 60°, , SM = MC
Доказать:
Найти:
Решение:
По теореме если одна из двух прямых лежит в плоскости, а другая прямая пересекает эту плоскость в точке, которая не принадлежит первой прямой, то данные прямые скрещивающиеся, так как и
прямые AM и BC - cкрещивающиеся.
По определению угол между скрещивающимися прямыми это угол между прямыми которые пересекаются и соответственно параллельны данным скрещивающимся прямым.
Так как по условию ABCD - квадрат, то по свойствам квадрата его противоположные стороны параллельны, тогда BC║AD. Так как BC║AD и прямые AM и DA имеют общую точку A, то по определению угла между скрещивающимися прямыми:
∠(AM,BC) = ∠(AM,AD) = 60°.
По теореме если прямая перпендикулярна к двум прямым, которые лежат в этой плоскости и пересекаются, то она перпендикулярна к этой плоскости, тогда AD ⊥ SCD, так как по условию ABCD квадрат, то по определению квадрата все его углы равны 90°, то есть
AD ⊥ CD и по условию SD ⊥ ABC, тогда по определению перпендикулярности прямой к плоскости, так как AD ⊂ ABC, то
SD ⊥ AD и CD ∩ SD = D.
Проведем отрезок MD.
По определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как AD ⊥ SCD и MD ⊂ SCD, то AD ⊥ MD, следовательно треугольник ΔMAD - прямоугольный.
По определению угол между прямыми принадлежит промежутку от 0° до 90° включительно, так как треугольник треугольник ΔMAD - прямоугольный, то угол ∠MAD < 90°, тогда ∠(AM,AD) = ∠MAD = 60°.
Пусть AD = x, тогда ВС = DC = AB = x, так как по свойствам квадрата все его стороны равны и по условию ABCD - квадрат.
Рассмотрим прямоугольный треугольник ΔMAD :
.
Рассмотрим прямоугольный треугольник ΔSCD (SD ⊥ CD). Так как по условию SM = MC, то по определению MD - медиана. По свойствам прямоугольного треугольника медиана проведенная к гипотенузе равна половине гипотенузы, то есть CM = MS = MD = .
По основному свойству отрезка:.
По теореме Пифагора:
.
.
По теореме о трех перпендикулярах AS ⊥ AB, так как AD ⊥ AB (по определению квадрата (ABCD) все его углы равны 90° ), SD ⊥ AD и отрезок AD - проекция отрезка AS на плоскость ABC в прямоугольном треугольнике ΔSAD.
Так как A ∈ (SAB,SAD) и S ∈ (SAB,SAD), то по аксиоме стереометрии плоскость SAD ∩ SAB = AS.
По теореме если прямая перпендикулярна к двум прямым, которые лежат в этой плоскости и пересекаются, то она перпендикулярна к этой плоскости, тогда AB ⊥ DAS, так как по условию по условию ABCD квадрат, то по определению квадрата все его углы равны 90°, то есть AB ⊥ DA и по теореме о трех перпендикулярах AB ⊥ AS и
AD ∩ SA = A.
По теореме если одна из двух плоскостей проходит через прямую, перпендикулярную ко второй плоскости, то эти плоскости перпендикулярны, так как AB ⊥ DAS и AB ⊂ SAB, то SAD ⊥ SAB.
Рассмотрим прямоугольный треугольник ΔSAD (SD ⊥ AD). Из точки D проведем высоту к гипотенузе в точку K, то есть DK ⊥ AS.
По теореме если две плоскости перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярна к прямой пересечения плоскостей, является перпендикулярной ко второй плоскости, тогда так как SAD ⊥ SAB, SAD ∩ SAB = AS и DK ⊥ AS по построению, то DK ⊥ SAB.
По определению расстояние от точки до плоскости есть перпендикуляр проведенной от этой точки к данной плоскости, тогда , так как DK ⊥ SAB.
Так как x = AD, то по условию , тогда:
.
Рассмотрим прямоугольный треугольник ΔSAD.
По теореме Пифагора:
По формулам площади для треугольника ΔSAD составим систему уравнений:
.