Предмет: Геометрия,
автор: KittyAlisa
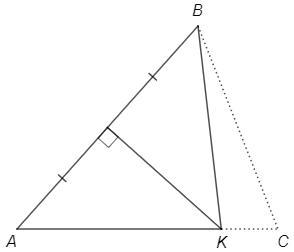
В треугольнике ABC отмечена точка K, в которой сторона AC пересекается с серединным перпендикуляром к стороне AB. Оказалось, что AK=BC+CK. Докажите, что треугольник ABC равнобедренный.
Ответы
Автор ответа:
1
Точка K на серединном перпендикуляре к AB, следовательно равноудалена от концов отрезка, AK=BK.
Тогда по условию BK=BC+CK.
В треугольнике BCK сумма двух сторон равна третьей стороне - треугольник вырожденный, точки B-C-K лежат на одной прямой.
(Или можно сказать, что расстояние между конечными точками ломаной B-C-K равно длине ломаной => ломаная вырожденная, точки B-C-K на одной прямой.)
По условию точка K лежит на отрезке AC. Несовпадающие прямые AC и BC могут иметь только одну общую точку, следовательно точки K и С совпадают.
Тогда вершина С лежит на серединном перпендикуляре к основанию AB, AC=BC, △ABC - равнобедренный.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ОМЛИОД
Предмет: Русский язык,
автор: ученик022016
Предмет: Русский язык,
автор: 23516
Предмет: Информатика,
автор: osmakova
Предмет: Другие предметы,
автор: DocBrayn1