Предмет: Алгебра,
автор: jobbline
докажите тождество 50 баллов
Приложения:
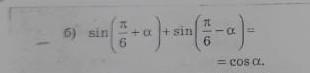
Ответы
Автор ответа:
0
Ответ:
Формула суммы синусов:
Похожие вопросы
Предмет: Русский язык,
автор: Foka11
Предмет: Русский язык,
автор: макс39101
Предмет: Русский язык,
автор: Аноним
Предмет: ОБЖ,
автор: TITANGEL