Предмет: Алгебра,
автор: somptueusement
помогите пожалуйста, решить уравнение
Приложения:
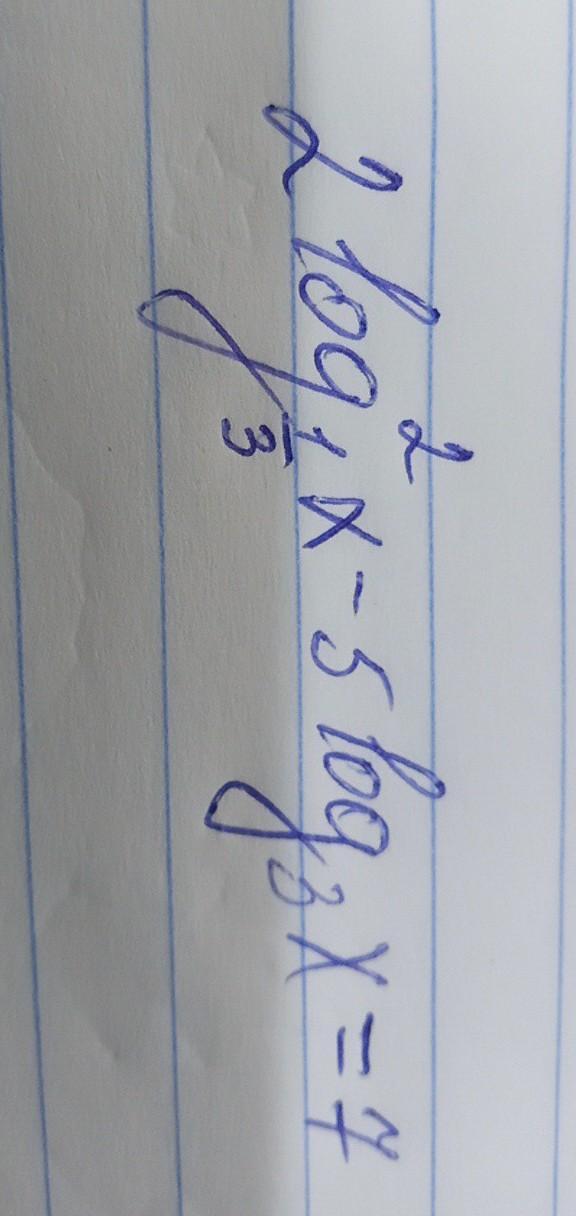
Simba2017:
пусть log(1/3)x=t
2t^2+5t-7=0
D=25+56=81
t1=(-5+9)/4=1; log(1/3)x=1; x1=1/3
t2=(-5-9)/4=-14/4=-3.5; x2=(1/3)^(-3.5)
большое спасибо
крайне вам благодарен
одз x>0. оба корня подходят
хорошо
x2=3^(7/2)=корень из 2187
Ответы
Автор ответа:
2
Ответ:
1/3 и 27√3
Объяснение:
О Д З : х > 0 ; преобразуем
З а м е н а
О б р а т н а я з а м е н а
и
Все корни подходят по ОДЗ.
больше спасибо
Похожие вопросы
Предмет: Русский язык,
автор: maskov1
Предмет: Русский язык,
автор: ученик1330
Предмет: Русский язык,
автор: Dasha17011989
Предмет: Английский язык,
автор: tanyamanzhureva
Предмет: Математика,
автор: Никита08092003