Предмет: Геометрия,
автор: friday10052020
СРОЧНО
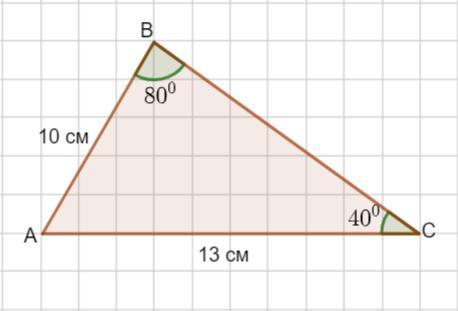
в треугольнике ABC стороны AB=10см AC=13см угол C=40 угол B=80 найдите площадь треугольника
Приложения:

Ответы
Автор ответа:
2
Ответ:
см ² - площадь треугольника ΔАВС.
Объяснение:
Пусть дан Δ АВС . ∠ С=40°, ∠В= 80°, АВ= 10 см, АС =13 см.
Так как сумма углов треугольника равна 180°, то найдем градусную меру ∠А.
∠ А= 180°- ( 40°+80°)=180°- 120° = 60°.
Найдем площадь треугольника как полупроизведение сторон треугольника на синус угла между ними
см².
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Olyqwerty
Предмет: Русский язык,
автор: асият5555
Предмет: Русский язык,
автор: zellooz
Предмет: Математика,
автор: mitroschinaanastasia
Предмет: Геометрия,
автор: ValeraDavay