Вышло так, что 13 программист (ов) живут вдоль одной прямой улицы, причём все их дома находятся с одной стороны от дороги. Расстояния между домами могут быть разными, могут - одинаковыми. Номера домов идут по порядку, начиная с единицы. Один из программистов высчитал, до какого дома сумма расстояний от всех других будет наименьшей, и предложил встретиться для настольной игры там. Что это за дом? (В ответе укажи номер.)
Ответы
Ответ:
Сумма расстояний от всех других домиков будет наименьшей до домика номер 7.
Пошаговое объяснение:
Определить, что это за дом, до которого сумма расстояний от всех других будет наименьшей.
По условию 13 домов. Расстояния между домами могут быть разными, могут - одинаковыми.
Сумма расстояний должна быть наименьшей, то есть сумма расстояний, которые пройдут программисты до искомого дома.
Рассмотрим задачу с меньшим количеством домиков, например, пятью.
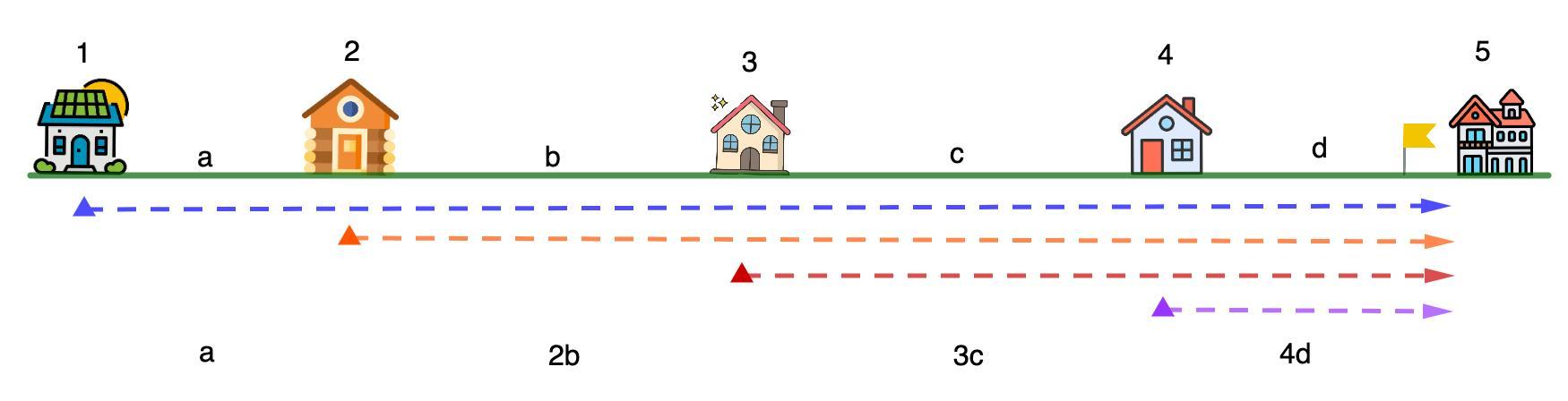
1) Обозначим расстояния между домиками, как a, b, c, d.
Выберем крайний домик.
Сумма расстояний, пройденными программистами будет равна:
a + 2b + 3c +4d
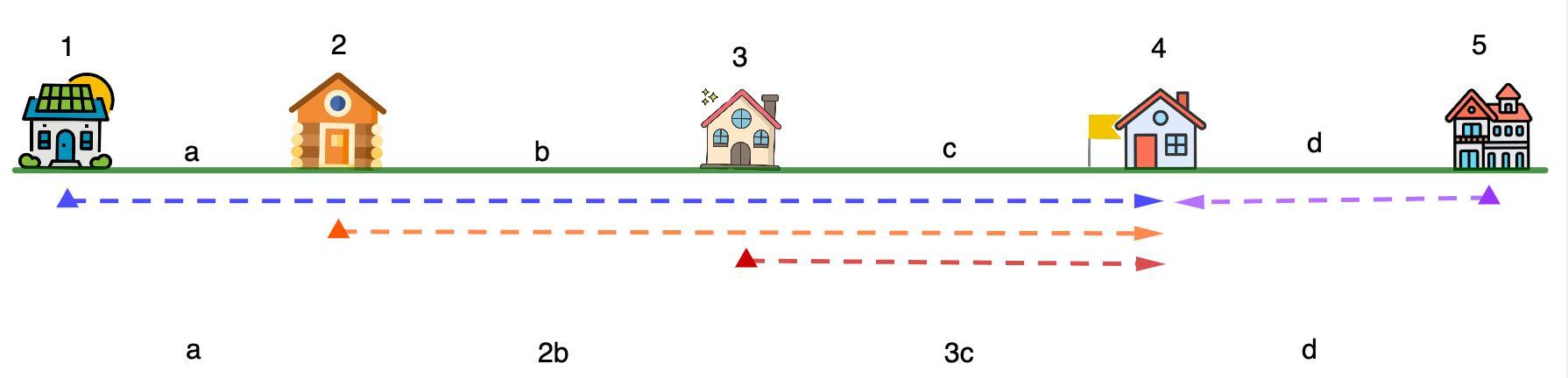
2) Теперь рассмотрим промежуточный вариант. Домик номер 4.
Получим сумму расстояний:
а + 2b + 3c + d
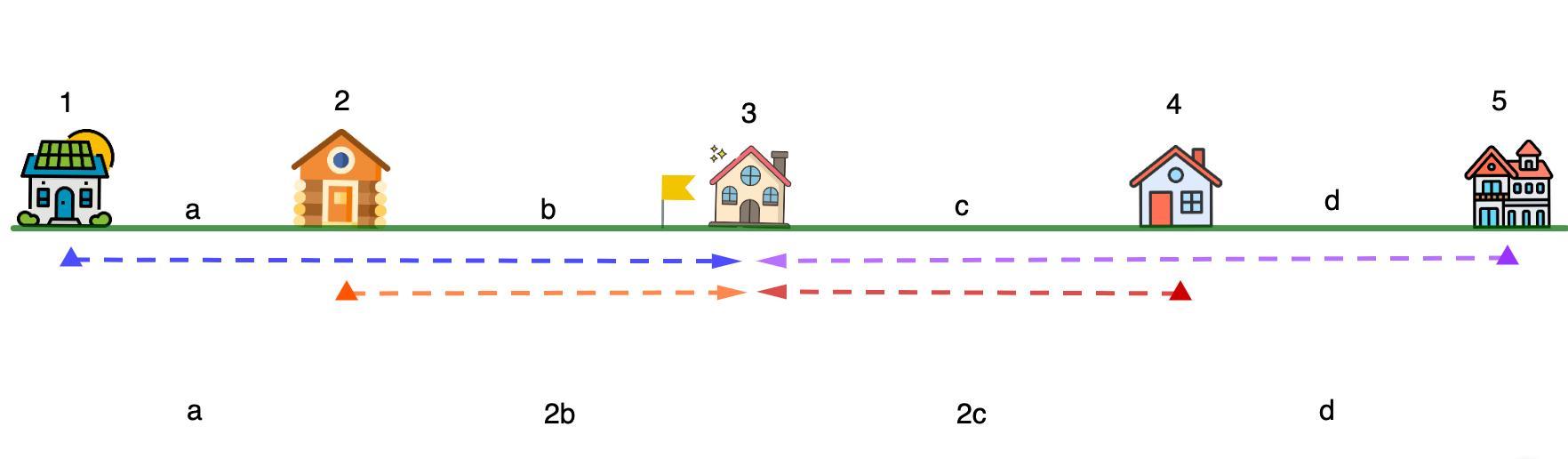
3) Теперь рассмотрим средний домик номер 3.
Здесь сумма расстояний будет равна:
a + 2b + 2c + d.
a + 2b + 2c + d < а + 2b + 3c + d < a + 2b + 3c +4d |-(a +2b)
2c + d < 3c + d < 3c +4d
См. вложения.
Получили, что сумма расстояний от всех других домиков будет наименьшей, если домик находится в середине.
Аналогично можно рассуждать для 13 домов.
В нашем случае центральный домик будет под номером 7.