Question

Помогите пожалуйста!
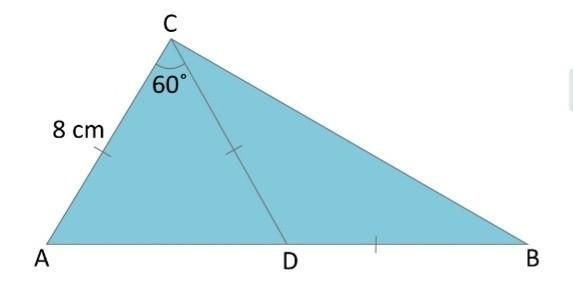
А) Сколько градусов угол B
a) 20° b) 30° c) 45° d) 60°

Б) Найти стороны AB длину
Если не сложно, желательно с объяснениями:)
Спасибо всем заранее!!​

Answer 1

Ответ:

А) Сначала работаем с треугольником АДС:

Так его боковые стороны равны, то это равнобедренный треугольник. То есть, угол А будет равен углу Д. Сумма всех углов треугольника- 180°. Угол А и угол Д мы возьмём как "х". Получается:

2х + 60 = 180

2х = 120

х = 60. Угол А/Д равен 60°.

Теперь работаем с треугольником СДВ. Угол Д. Он соединяет 2 треугольника. Это смежный угол. Сумма смежных углов равна 180. Если мы знаем угол АДС, то модем найти угол СДВ. 180-60 = 120°. Та же схема. Этот треугольник СДВ равномерный. Вершина нам известна (120°). Боковые стороны возьмём как 2х. Получается:

2х + 120 = 180

2х = 60

х = 30. Это угол В/С (угол В и С равны)

Б) Так как у нас получилось, что угол А/Д в треугольнике АСД равны, то получается стлрона АД тоже равна 8 см. Получается: АС = СД = АД = ДВ. То есть, ДВ равна 8, и АД равна 8.

АВ = 8+8 = 16 см

Answer 2

Ответ:

Сумма внутренних углов треугольника 180°.

а) так как треугольник ACD равнобедренный, углы при основании равны (угол CAD=угол ADC)

$\angle CAD + \angle ADC + \angle ACD= {180}^ {\circ}$

$\angle CAD + \angle ADC + {60}^{ \circ} = {180}^{ \circ}$

$\angle CAD + \angle ADC = {180}^{ \circ} - {60}^{ \circ} \\ \angle CAD + \angle ADC = {120}^{ \circ}$

$\angle CAD = \angle ADC = \frac{ {120}^{ \circ} }{2} = {60}^{ \circ}$

Значит треугольник ACD – равносторонний.

AC=AD=CD

Углы ADC и BDC – смежные, то есть их сумма 180°.

$\angle ADC +\angle BDC = {180}^ {\circ} \\ {60}^{ \circ} + \angle BDC = {180}^{ \circ} \\ \angle BDC = {180}^{ \circ} - {60}^{ \circ} \\ \angle BDC = {120}^{ \circ}$

Треугольник BDC тоже равнобедренный, значит угол BCD=угол CBD

$\angle BCD+ \angle CBD + \angle BDC= {180}^ {\circ} \\ \angle BCD+ \angle CBD + {120}^{ \circ} = {180}^{ \circ} \\ \angle BCD+ \angle CBD = {60}^{ \circ}$

$\angle BCD = \angle CBD = \frac{ {60}^{ \circ} }{2} = {30}^{ \circ}$

Угол B=30°.

б) как раньше упоминал треугольник ACD – равносторонний (все стороны равны), значит AD=8.

По условию CD=BD, значит BD=8.

AB=AD+BD=8+8=16

AB=16 см