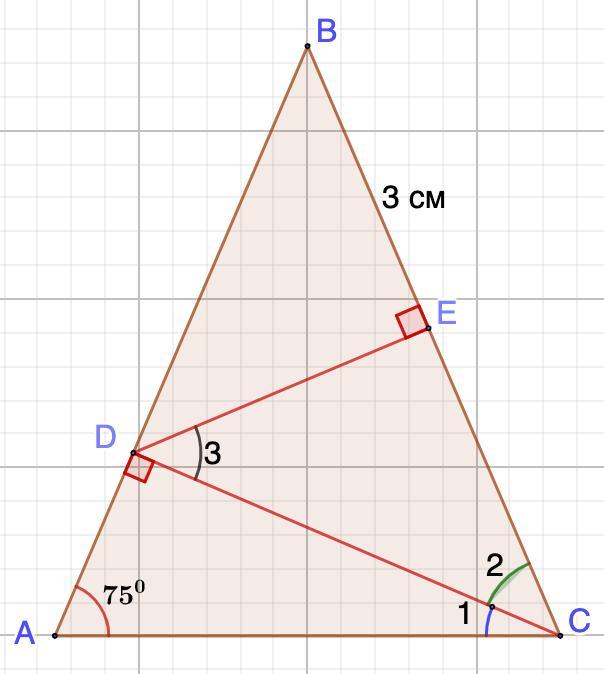
В равнобедренном треугольнике ABC с основанием AC угол A составляет 75°, из угла C построен перпендикуляр CD к противолежащей стороне, точка D лежит на стороне AB. Из точки D построен перпендикуляр DE к стороне BC, точка E лежит на стороне BC. Известно, что отрезок BE равен 3 см. Найди отрезок EC.
Ответы
Ответ:
Отрезок ЕС равен 1 см.
Объяснение:
Требуется найти отрезок ОС.
Дано: ΔАВС - равнобедренный;
∠А = 75°;
CD ⊥ АВ; DE ⊥ BC;
ВЕ = 3 см.
Найти: ЕС.
Решение:
1. Рассмотрим ΔΔАВС - равнобедренный;
- Углы при основании равнобедренного треугольника равны.
⇒ ∠А = ∠С = 75°
- Сумма углов треугольника равна 180°.
⇒ ∠В = 180° - (75° + 75°) = 30°
2. Рассмотрим ΔDBE - прямоугольный.
∠В = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
Пусть DE = x см, тогда DB = 2x см.
По теореме Пифагора:
BD² = DE² + BE²
4x² = x² + 9
3x² = 9
x² = 3
x = √3
DE = √3 см
3. Рассмотрим ΔАDC - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠1 = 90° - ∠А = 90° - 75° = 15°
4. Рассмотрим ΔEDC - прямоугольный.
∠2 = ∠С - ∠1 = 75° - 15° = 60°
∠3 = 90° - ∠2 = 90° - 60° = 30°
Пусть ЕС = у см, тогда DC = 2у см (катет, лежащий против угла 30°)
По теореме Пифагора:
DC² = DE² + EC²
4y² = 3 + y²
3y² = 3
y² = 1
y = 1
Отрезок ЕС равен 1 см.