Предмет: Алгебра,
автор: shabanov44hr
Решить через дискрименант
Приложения:
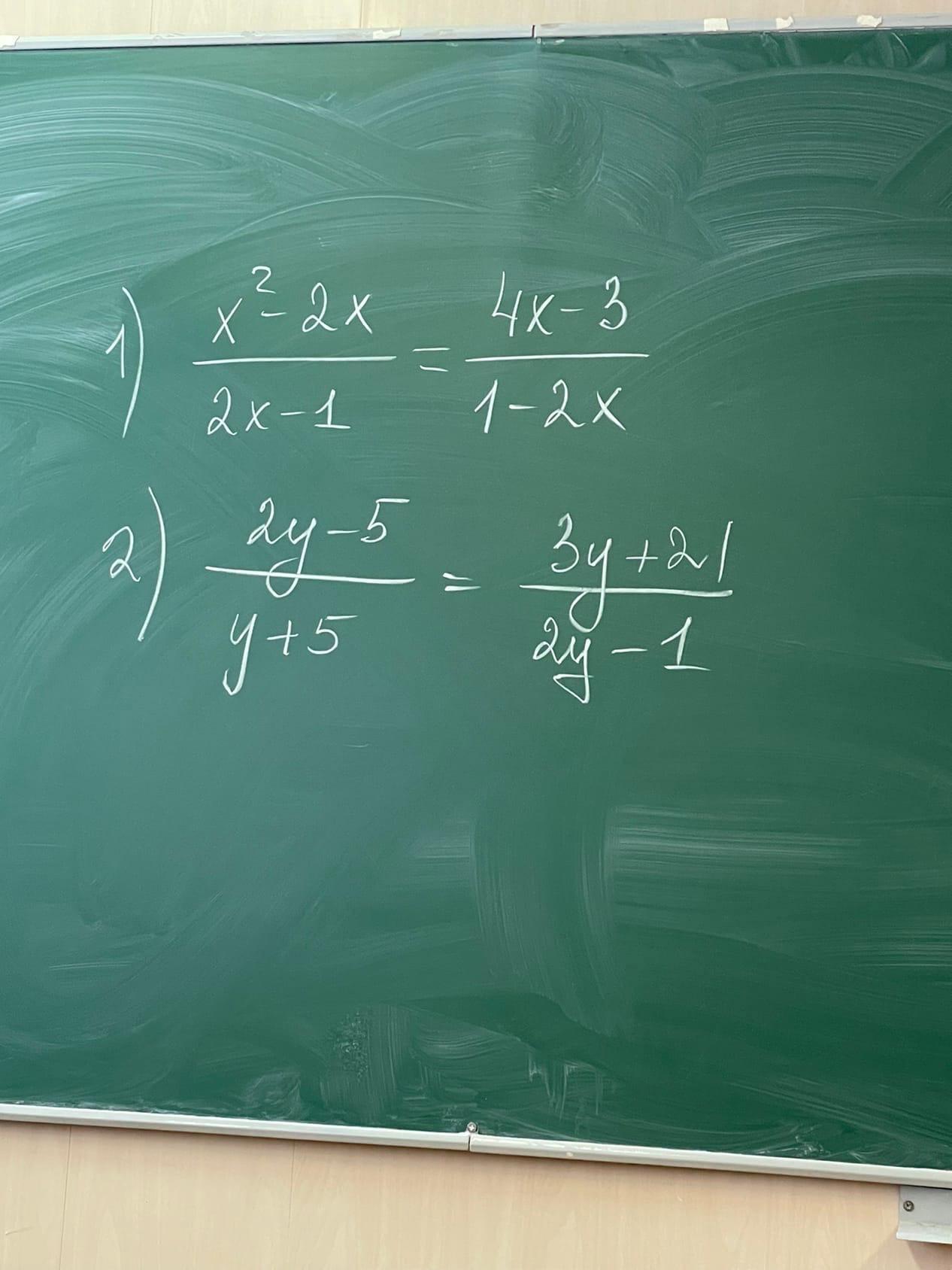
Ответы
Автор ответа:
0
Ответ:
Изучите теорему Виета, эти задания решаются намного легче именно через теорему Виета
EADF:
надеюсь, вам понравится оформление ответа. Если я вам помог, поставьте лайк, 5 звёзд и Лучший ответ :)
Похожие вопросы
Предмет: Английский язык,
автор: veronika08032005
Предмет: Английский язык,
автор: вера388
Предмет: Английский язык,
автор: Висиль
Предмет: Другие предметы,
автор: DrozdSvoboda
Предмет: Математика,
автор: munisa2006