Question

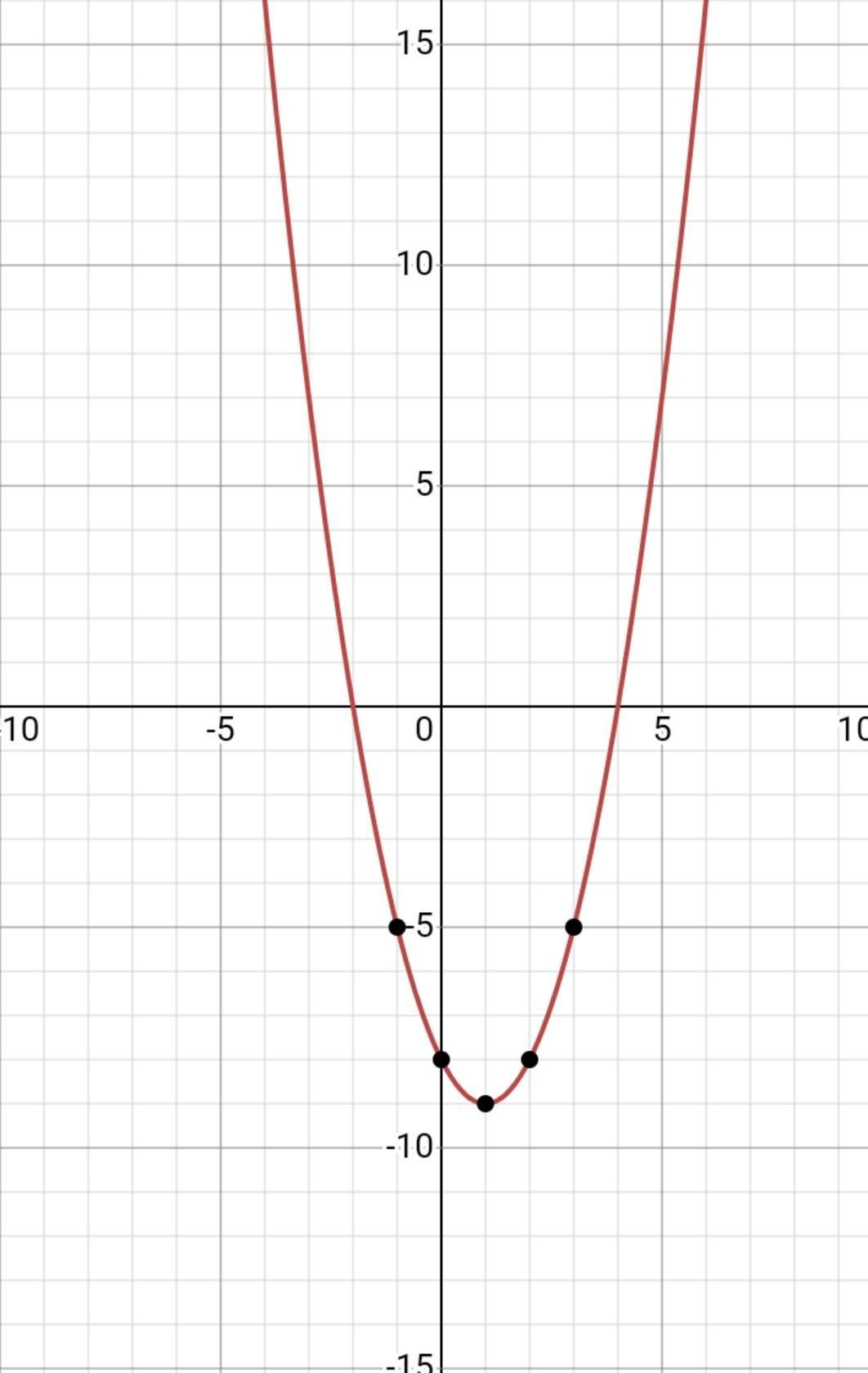
1. Дана функция: у = х^2 - 2x – 8
а) запишите координаты вершины параболы;
b) определите, в каких четвертях находится график функции;
с) запишите ось симметрии параболы; d) найдите точки пересечения графика с осями координат;
е) постройте график функции.​

Answer 1

Объяснение:

У=х^2-2х-8

а)

Х= - b/2a

X= - (-2)/2×1=2/2=1

y=1^2-2×1-8=1-2-8= - 9

(1 ; - 9) вершина

б)

Во всех четвертях

с)

Х= - b/2a

X= - (-2)/2×1=2/2×1=1

X=1 ось симметрии

d)

Х=0

У=0^2-2×0-8= - 8

(0; - 8) точка пересечения с осью у

У=0

х^2-2х-8=0

D=(-2)^2-4×1×(-8)=4+32=36

X1=(2-6)/2= - 2

X2=(2+6)/2=4

y1=(-2)^2-2×(-2)-8=4+4-8=0

y2=4^2-2×4-8=16-8-8=0

(-2;0) (4;0) точки пересечения с осью х

е) на рисунке

Х - 1 0 1. 2 3

У - 5 - 8 - 9 - 8 - 5