Предмет: Алгебра,
автор: alinaabasova75
49. (02-3-65) Вычислите.

Приложения:
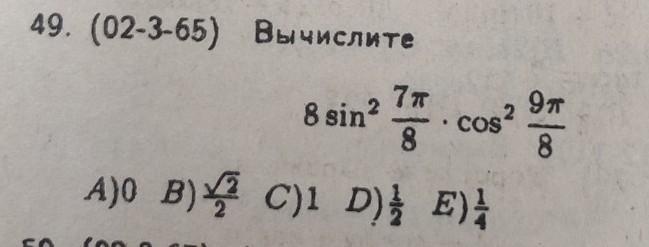
Ответы
Автор ответа:
2
Ответ:
ответ С
Объяснение:
8*синус в квадрате (пи /8)*косинус в квадрате(пи/8)=8*0.25*синус в квадрате (пи/4)=2*(корень из 2 /2) в квадрате=2*0,5=1
msuluzhan47:
апа
Автор ответа:
7
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: halberanna
Предмет: Русский язык,
автор: remmovik
Предмет: Физика,
автор: Ivanbarankin