Предмет: Алгебра,
автор: alinaabasova75
45. Найдите наибольшее значение выражения.

Приложения:
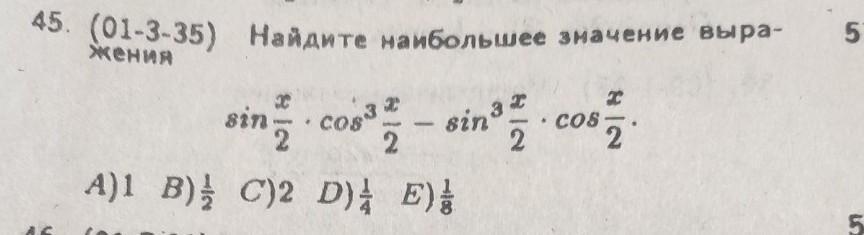
Ответы
Автор ответа:
1
alinaabasova75:
СПАСИБО ОГРОМНОЕ♡♡♡
Пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: lpkoptelova
Предмет: Русский язык,
автор: marinich1104
Предмет: Окружающий мир,
автор: ритамаргарита2
Предмет: Другие предметы,
автор: david2958
Предмет: Французский язык,
автор: hiha68