Предмет: Геометрия,
автор: pasha33735
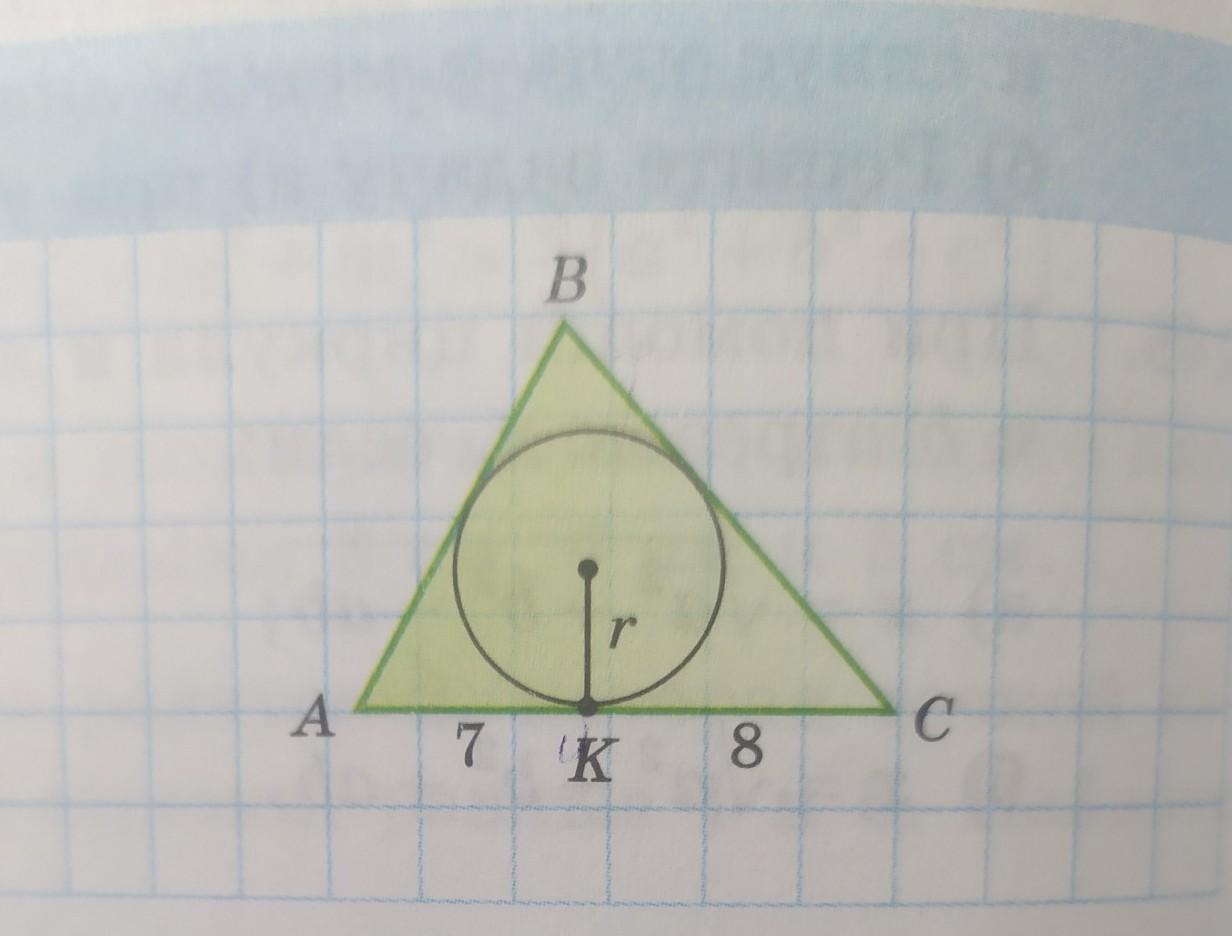
Найдите радиус вписанной окружности треугольника ABC, если его периметр равен 42 и AK = 7, KC = 8.
Приложения:
Ответы
Автор ответа:
1
Ответ:
4
Объяснение:
от точки С до двух точек касания соответственно будет одинаковое расстояние 8, от точки А расстояние до точек касания по 7, от точки В - например, по х. тогда АС=7+8=15, ВС=х+8; АВ=х+7, а периметр х+8+х+7+15, тогда полупериметр равен исходя из условия 42/2=21, а складывая все стороны треугольника и деля сумму на два, получим 21=х+15;
откуда х=6, тогда по Герону площадь равна
√((21*(21-15)*(21-7-6)(21-6-8))=√((21*6*8*7))=7*3*4=84; а по формуле через радиус вписанной окружности эта же площадь равна произведению полупериметра на радиус, который подлежит определению.
21*r=84⇒r=84/21=4
Похожие вопросы
Предмет: Окружающий мир,
автор: ярапро
Предмет: Окружающий мир,
автор: 546474546
Предмет: Английский язык,
автор: 0Ирина01
Предмет: Математика,
автор: anastassiaandrijevsk