Question

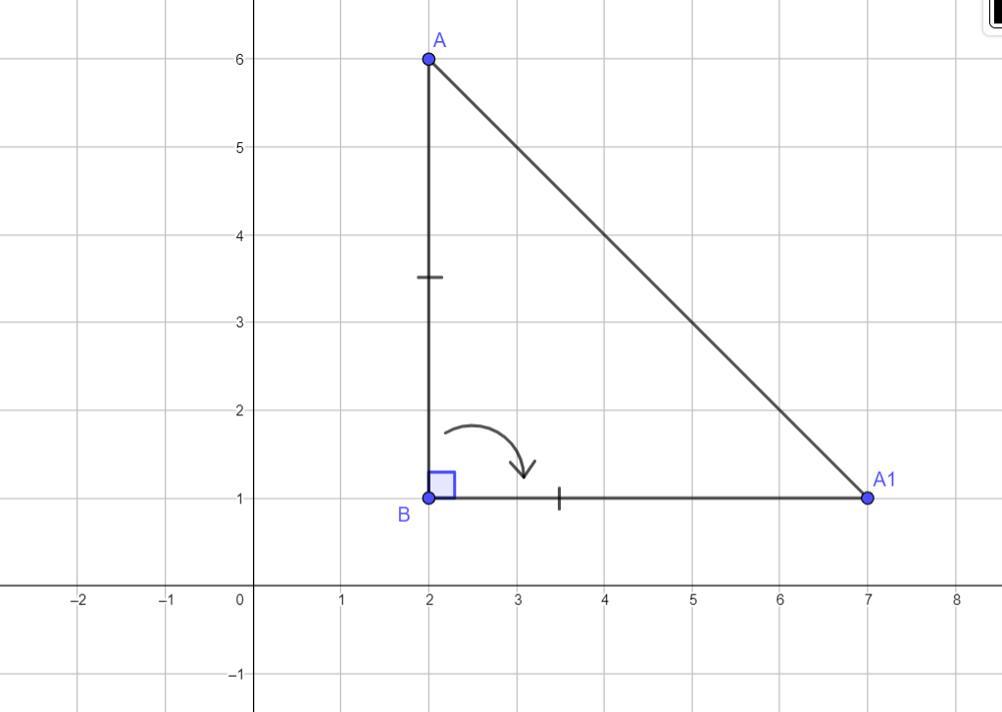
На координатной плоскости отмечены точки A(2;6),B(2;1). отрезок AB повернули вокруг точки B на 90 градусов по часовой стрелке и получили отрезок A1 B. Найдите площадь фигуры AA1B.

Answer 1

Найдем расстояние между точками A и B:

$AB = \sqrt{(x_B - x_A)^2 +(y_B-y_A)^2} =\sqrt{(2-2)^2 + (1-6)^2} =\sqrt{25} =5$.

Построим отрезок A1B, образованный поворотом отрезка AB вокруг точки B на 90 градусов по часовой стрелке.

При повороте отрезок отображается на равный ему отрезок, поэтому A₁B = AB = 5.

Соединим точки A и A1, чтобы получить фигуру AA₁B.

Эта фигура — прямоугольный треугольник (∠B = 90°) с катетами, равными 5.

Площадь прямоугольного треугольника — это половина произведения его катетов, поэтому:

$\displaystyle S_{\triangle AA1B} = \frac{AB \cdot A_1B}{2}=\frac{5\cdot 5}{2}=\frac{25}{2}= 12,5.$

Ответ: $S_{\triangle AA1B} = 12,5.$