Question

в равнобедренной трапеции abcd меньшее основание bc=7 один из углов трапеции равен 121° боковая сторона равна 9. найдите площадь трапеции​

Answer 1

Ответ:

площадь трапеции​ равна 63cos31° + $\frac{81}{2}$sin62° , что приблизительно равно 89.76

Объяснение:

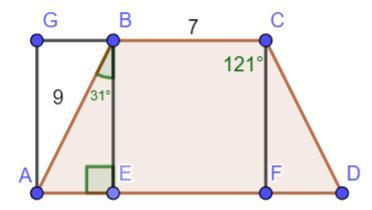
Достроим рисунок высотами BE и CF.

Отметим, что площадь трапеции ABCD будет совпадать с площадью прямоугольника AFCG = AF*CF = (AE+EF)*BE = (7+AE)*BE

∠ABC=∠CBD=121° , ∠EBC=90°  значит ∠ABE=31°

В прямоугольном треугольнике ABE

sin∠ABE=AE/AB     ⇒ sin31°=AE/9       ⇒  AE=9*sin31°

cos∠ABE=BE/AB     ⇒ cos31°=BE/9       ⇒  BE=9*cos31°

Значит искомая площадь = (7+AE)*BE = (7+9*sin31°)*9*cos31° =

= 63cos31° + 81sin31°cos31° = 63cos31° + $\frac{81}{2}$sin62° ≈ 89.76