Question

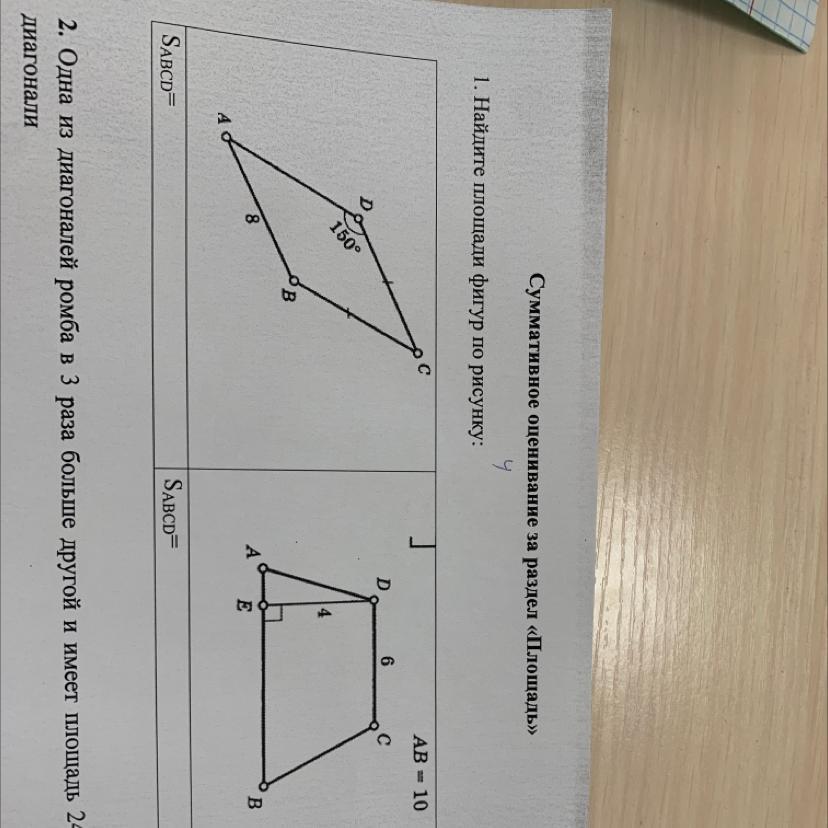
1. Найдите площади фигур по рисунку:
с
AB = 10
D
6
с
150°
4
В
B
E
SABCD=
SABCD=
Дам 35

Answer 1

Ответ:

Дано: ABCD - параллелограмм, AB = 6, BC = 8, ∠B = 150°

Найти: S параллелограмма

Решение:

∠B = 150°

Значит, ∠A = 180°-150° = 30° (свойства параллелограмма)

Проведем из вершины B прямую, перпендикулярную AD (высоту), назовем её BH. У нас образуется прямоугольный треугольник ABH.

BH = 1/2 гипотенузы AB, потому что лежит напротив угла в 30°

BH = 1/2 * 6 = 3

Финальный этап, находим площадь.

S = a * h

S = AD * BH

S = 8 * 3 = 24.

Ответ: 24 (см)

Answer 2

Ответ:

1. 32; 2. 32

Объяснение:

Площадь первой фигуры можно найти по формуле.

${x}^{2} \sin(a)$

где x - сторона

Но для начала необходимо найти угол a, для этого необходимо сделать:

$\frac{360 - 150 + 150}{2} = 30$

Мы нашли угол BAC и BCD, теперь всё можно подставлять в формулу.

${8}^{2} \sin(30) = 32$

Для решения второй задачи необходимо воспользоваться формулой по нахождению площади трапеции.

$\frac{10 + 6}{2} \times 4 = 32$