Вычислить площадь фигуры, ограниченной линиями(пожалуйста, понятно и подробно)
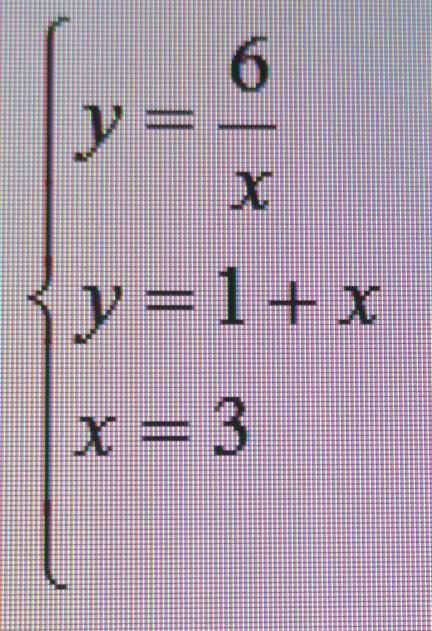
Ответы
Ответ:
Площадь фигуры, ограниченной линиями равна (ед.²)
Пошаговое объяснение:
Требуется вычислить площадь фигуры, ограниченной линиями.
Площадь фигуры вычислим по формуле:
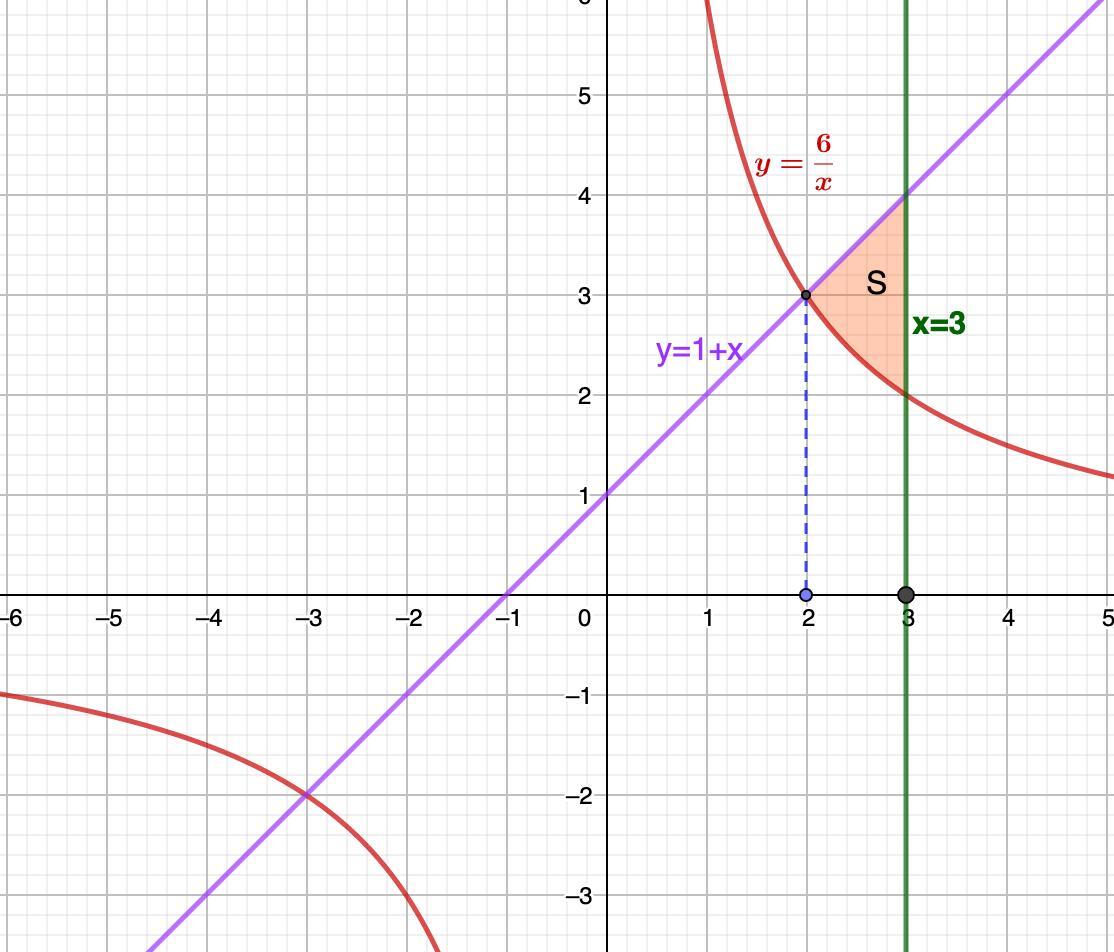
Построим графики и определим фигуру, площадь которой надо вычислить.
1.
- функция обратной пропорциональности, график - гипербола, расположена в 1 и 3 четвертях.
Возьмем несколько точек:
x = 1; y = 6;
x = 2; y = 3;
x = 3; y = 2;
x = 6; y = 1.
Строим ветвь гиперболы, вторую строим симметрично начала координат.
2. y = 1 + x
- линейная функция, график прямая.
Достаточно двух точек:
х = 0; у = 1;
х = 2; у = 3.
Строим график.
3. х = 3
- прямая, параллельная оси 0у.
4. Найдем точки пересечения первых двух графиков:
По теореме Виета:
х₁ = 2; х₂ = -3
5. Нашли искомую фигуру, ограниченную данными линиями:
Сверху: f₂(x) = 1 + x
Снизу:
Слева: a = 2
Справа: b = 3
6. Теперь можем найти площадь:
Площадь фигуры, ограниченной линиями равна (ед.²)