Предмет: Геометрия,
автор: suchkovataisiya
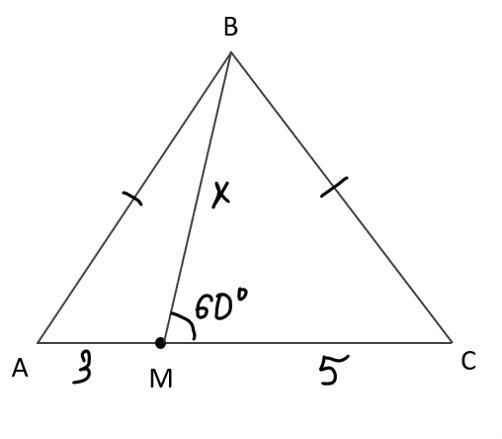
на основании ас равнобедренного треугольника авс взяли такую точку м что угол вмс равен 60 найдите вм если ам равно 3 а см равно 5
BortovoJ:
ахаахаха, прими запрос в друзья
Ответы
Автор ответа:
3
Так как АВС — равнобедренный треугольник с основанием АС, то АВ = ВС.
∠BMC + ∠BMA = 180°, поскольку они смежные.
Значит, ∠BMA = 180 - ∠BMC = 180 - 60 = 120°.
По теореме косинусов:
.
.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятого с противоположным знаком, поэтому:
;
.
Подставляем известные величины в формулы. BM обозначим как x.
Раз длины сторон АВ и ВС равны, то их квадраты тоже будут равны, так что можем приравнять полученные выражения:
;
.
Ответ: BM = 2 см.
Приложения:
а можно без косинусов
Внатуре давай без них
Похожие вопросы
Предмет: Українська мова,
автор: Puding18
Предмет: Українська мова,
автор: yolkayoyo
Предмет: Українська література,
автор: ketriiin25
Предмет: Математика,
автор: kalinicheva13