Предмет: Алгебра,
автор: Аноним
найдите значение производной функции f(x)в точке x0
Приложения:
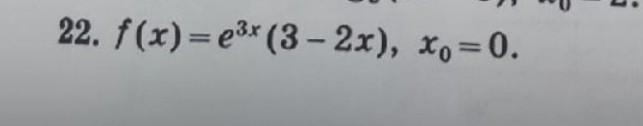
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Приложения:


Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: RalphWiggum
Предмет: Английский язык,
автор: pcheremnykh
Предмет: Информатика,
автор: Zehnder
Предмет: Русский язык,
автор: 20033028