Предмет: Математика,
автор: annadeevanss
Помогите даю много баллов КОМБИНАТОРИКА, уравнение
Приложения:
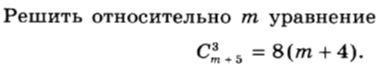
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Число сочетаний:
Автор ответа:
0
Ответ:mCC3CC3C
Пошаговое объяснение:m=1 c 3/6=20
Похожие вопросы
Предмет: Русский язык,
автор: БибиКимкай
Предмет: Русский язык,
автор: aishaadilova
Предмет: Окружающий мир,
автор: alinamyxa098
Предмет: Математика,
автор: deva70
Предмет: Психология,
автор: DerFoxn