Предмет: Алгебра,
автор: nahuishkoly
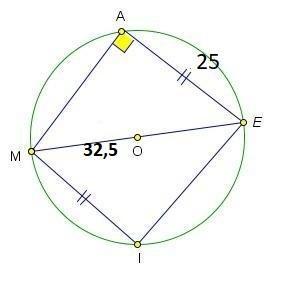
На окружности с центром в точке О по порядку отмечены 4 точки: А, Е, І, М. Найди вторую сторону получившегося четырёхугольника, если AE || MI, AE MI, радиус этой окружности 32,5 см, а АЕ 25 см.
zveryakovanata:
Уточните. AE || MI, а вот что про AE и MI известно?
Параллельныили равны?
Ответы
Автор ответа:
3
Ответ: 60 см
Объяснение: Дано:AEIM четырехугольник, А, Е, І, М∈ окр(O; R), АЕ=25 см, AE || MI, АМ║ EI, R=32,5 cм Найти АМ
1) AEIM - параллелограмм по свойству параллельности противоположных сторон; ⇒AE = MI=25 см, АМ= EI, МЕ-общая, ⇒ ΔМАЕ=ΔEIM по трём сторонам
2) ∠MAE =∠MIE
Но у вписанного четырёхугольника сумма противоположных углов равна 180°, т.е. ∠MAE +∠MIE =180° ⇒ ∠MAE =∠MIE =90°
3)∠ MAE - прямой, значит он опирается на диаметр. значит ME - диаметр окружности МЕ =2R=2·32,5=65 (см)
4) ⇒Δ MAE - прямоугольный, ∠MAE=90°, AE=25, ME=65
По теореме Пифагора:
AM²+AE²=ME²
AM²+25²=65²
AM²=4225-625=3600
AM=√3600=60 (см)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: tetyninhutir
Предмет: Українська література,
автор: zhmurrr
Предмет: Українська мова,
автор: Богдан213213213
Предмет: Математика,
автор: Lushnikov2552
Предмет: Русский язык,
автор: Shkolnik7727