Предмет: Алгебра,
автор: alinaabasova75
12. (97-10-56) Упростите выражение.

Приложения:
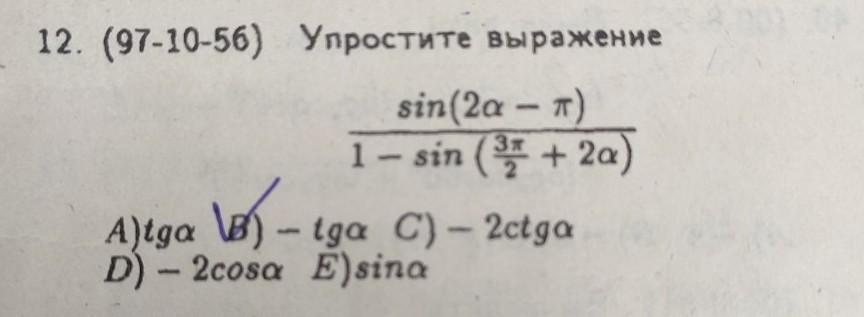
Ответы
Автор ответа:
6
Ответ: B) -tgα
Объяснение:
используя нечетность синуса (sin(2α-π)=-sin(π-2α);
формулу синуса двойного аргумента sin2α=2sinα*cosα, формулы приведения, формулу 1+cos2α=2cos²α; получим
(sin(2α-π))/(1-sin((3π/2)+2α)=-sin(π-2α)/(1+cos2α)=(-sin2α)/(2сos²α)=
-2sinα*cosα/(2cos²α)=-sinα/cosα=-tgα
Автор ответа:
7
Ответ:
Используем нечётноcть синуса ,формулы приведения, формулы двойных углов .
Похожие вопросы
Предмет: Русский язык,
автор: СашаМинина
Предмет: Окружающий мир,
автор: il9891
Предмет: Русский язык,
автор: Музa24com
Предмет: Математика,
автор: Vasilissa2007
Предмет: Алгебра,
автор: tolya26042005tolya