Question

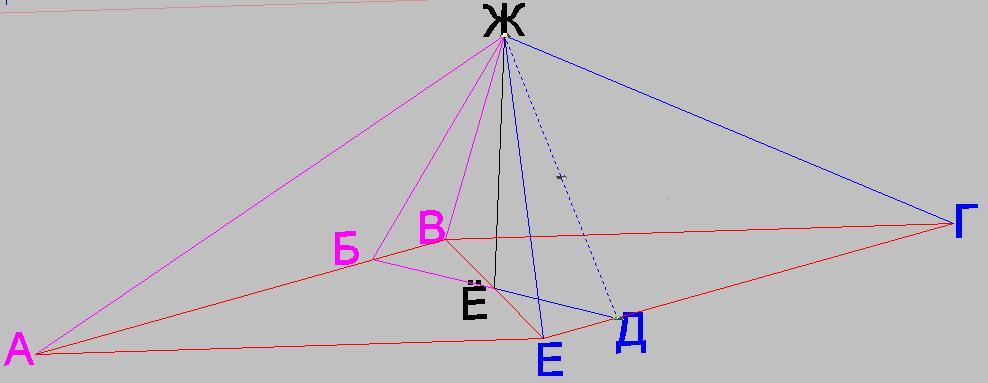
помогите с задачей по геометрии
Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности пирамиды.

Answer 1

Ответ:

Объяснение:

По условию

АЕ = 4 м

АВ = 5 м

ВЕ = 3 м

ЁЖ = 2 м

1. Площадь основания

Треугольник АВЕ прямоугольный со сторонами 3, 4, 5,

ВЕ является высотой параллелограмма АВГЕ

S(АВГЕ) = АЕ*ВЕ = 4*3 = 12 м²

2. Найдём вторую высоту параллелограмма БД

S(АВГЕ) = АВ*БД = 5*БД = 12

БД = 12/5 = 2,4 м

3. Площадь треугольника АЕЖ и равного ему ВГЖ

Треугольник АЕЖ - прямоугольный с прямым углом Е

Длину катета ЕЖ найдём по т. Пифагора из треугольника ЕЁЖ

ЕЁ = 1/2*ВЕ = 3/2 м

ЕЖ² = ЕЁ² + ЁЖ² = 1,5² + 2² = 6,25

ЕЖ = 2,5 м

S(АЕЖ) = 1/2*AE*EЖ = 1/2*4*2,5 = 5 м²

4. Площадь треугольника ГЕЖ и равного ему АВЖ

Высоту ДЖ треугольника ГЕЖ найдём по т. Пифагора из треугольника ЁЖД

ЁД = 1/2*БД = 2,4/2 = 1,2 м

ЖД² = ЁД² + ЁЖ² = (1,2)² + 2² = 5,44 м²

ЖД = √5,44  = 2√34/5 м

S(ГЕЖ) = 1/2*EГ*ЖД = 1/2*5*2√34/5 = √34 м²

5. Полная поверхность пирамиды

S = 12 + 2*5 + 2*√34 = 22+2√34 м²