Предмет: Геометрия,
автор: leriapronuskina
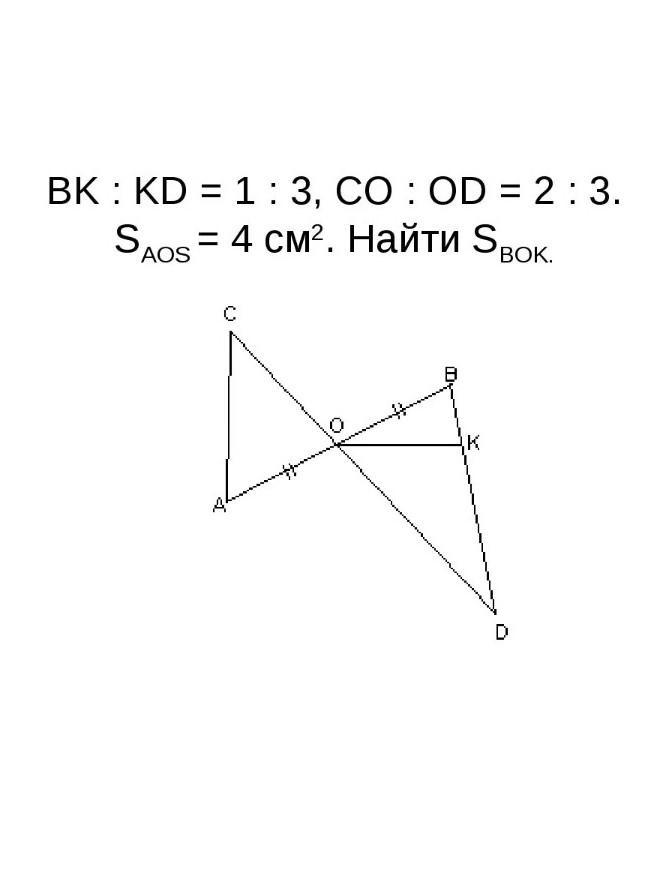
помогите пожалуйста решить
Приложения:
Ответы
Автор ответа:
0
Ответ:
3/2 см^2
Объяснение:
1. Найдём площадь треугольника BOD
∠BOD = ∠AOC как вертикальные углы
AO = BO по условию
2. Найдём отрезок BK
KD = 3*BK
BD = BK + KD = BK + 3*BK = 4*BK
BK = BD/4
3. Искомая площадь
Треугольники BOK и BOD имеют общую высоту h, построенную от прямой BK к вершине О. Поэтому их площадь пропорциональна длинам оснований
Похожие вопросы
Предмет: Русский язык,
автор: соня968
Предмет: Русский язык,
автор: AminaPro
Предмет: Русский язык,
автор: вита113
Предмет: Математика,
автор: Рафа06
Предмет: Математика,
автор: masha376818