Предмет: Алгебра,
автор: liana8543
Помогите найти сумму первых пяти членов геометрической прогрессии
Приложения:
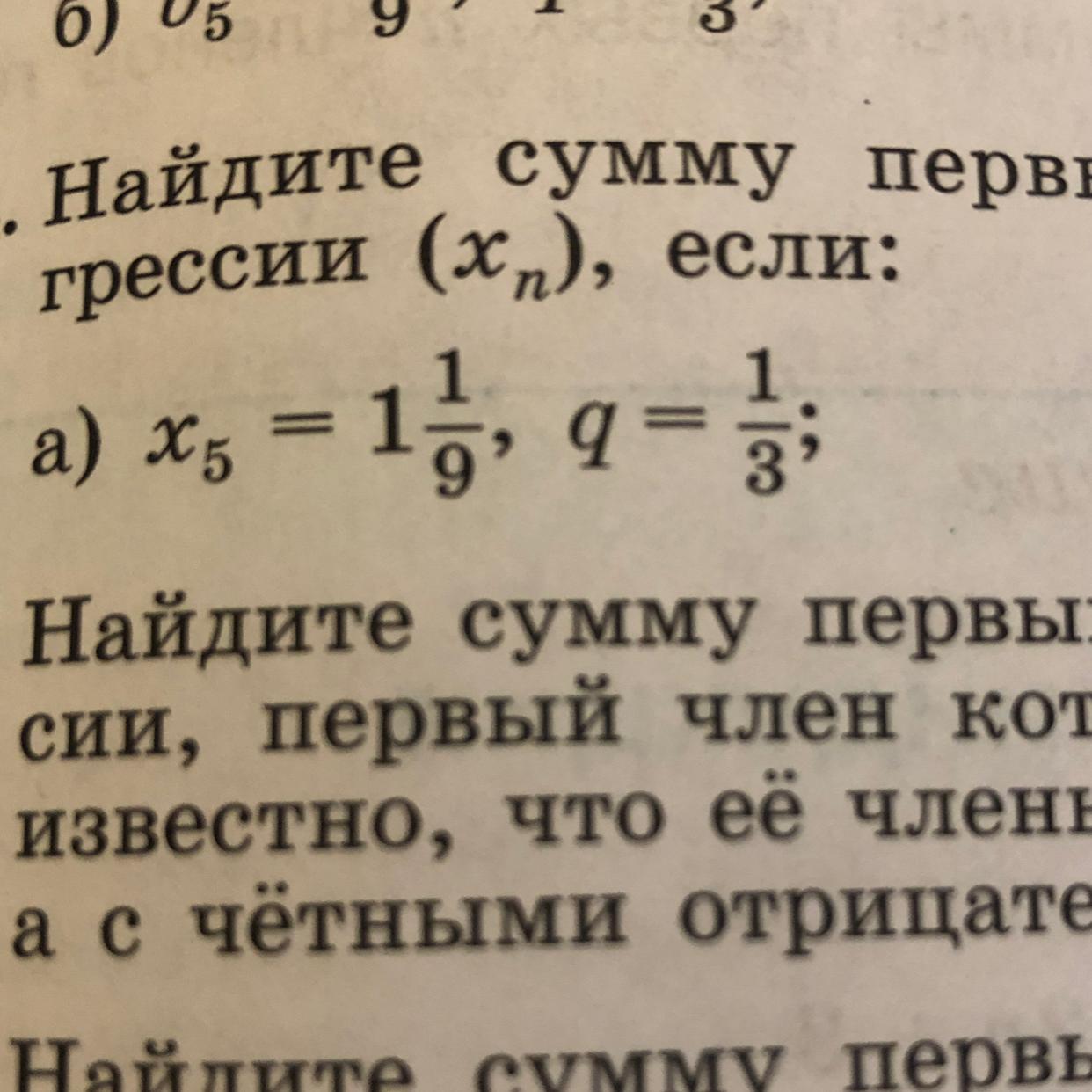
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Найдём первый член прогрессии
Сумма n первых членов геометрической прогрессии
Похожие вопросы
Предмет: Окружающий мир,
автор: vitzaton
Предмет: Русский язык,
автор: Умная12311
Предмет: Қазақ тiлi,
автор: 1234740
Предмет: Обществознание,
автор: Холодд