имеем последовательность (xn)...
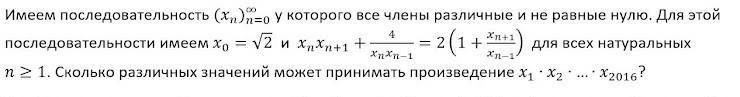
Ответы
Ответ:
1
Объяснение:
Преобразуем равенство:
Т.е. выполнено хотя бы одно из равенств: либо
, либо
.
Заметим, что одновременно они выполняться не могут, ведь тогда - противоречие с тем, что все члены посл-ти различны.
Значит, выполнено ровно одно из равенств.
В случае второе равенство примет вид
- противоречие с тем, что все члены посл-ти различны. Значит для
верно первое равенство, и
.
Также заметим, что для двух последовательных индексов верны различные равенства, ведь иначе, в первом случае, , а во втором
- в обоих случаях противоречие с тем, что все члены посл-ти различны.
В совокупности, это означает, что , откуда однозначно
, т.е. принимает одно значение, если такая последовательность вообще существует.
Легко привести пример такой последовательности:
, т.е.
-
- единственный иррациональный член, на нечетных местах стоят нечетные натуральные числа, равные номеру места, а на четных - дробь с числителем 2 и знаменателем, содержащим нечетное число, равное номеру предыдущего члена - т.е. между собой члены с четными номерами также различны, а их значение не может оказаться равным какому-либо из нечетных чисел, занятых нечетными членами.