Предмет: Алгебра,
автор: oKIRIGIRIoSANo
дана функция f: R->R, для которой справедливо неравенство...
Приложения:
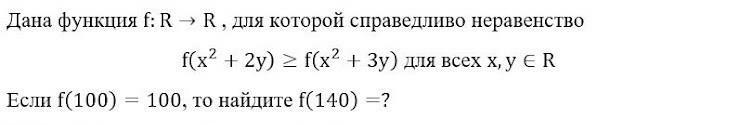
Аноним:
ответ точно не 140
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Очевидной идеей является связать значения аргумента 100 и 140 со значениями аргумента в неравенстве.
Заметим, что разница между аргументами функции в неравенстве по модулю равна . Поэтому рассмотрим 2 частных случая:
1) положим . Отсюда
. Положив теперь
, получим
.
2) положим . Отсюда
. Положив теперь
, получим
.
Но полученные 2 неравенства возможны лишь если . Тогда, согласно условию,
.
Похожие вопросы
Предмет: Другие предметы,
автор: sokka2001
Предмет: Английский язык,
автор: викторияхах
Предмет: Русский язык,
автор: Владушон
Предмет: Математика,
автор: mikalok
Предмет: Английский язык,
автор: sofka147