Предмет: Алгебра,
автор: anutasakalanskaa
Пожалуйста помогите решить задачи!!!!
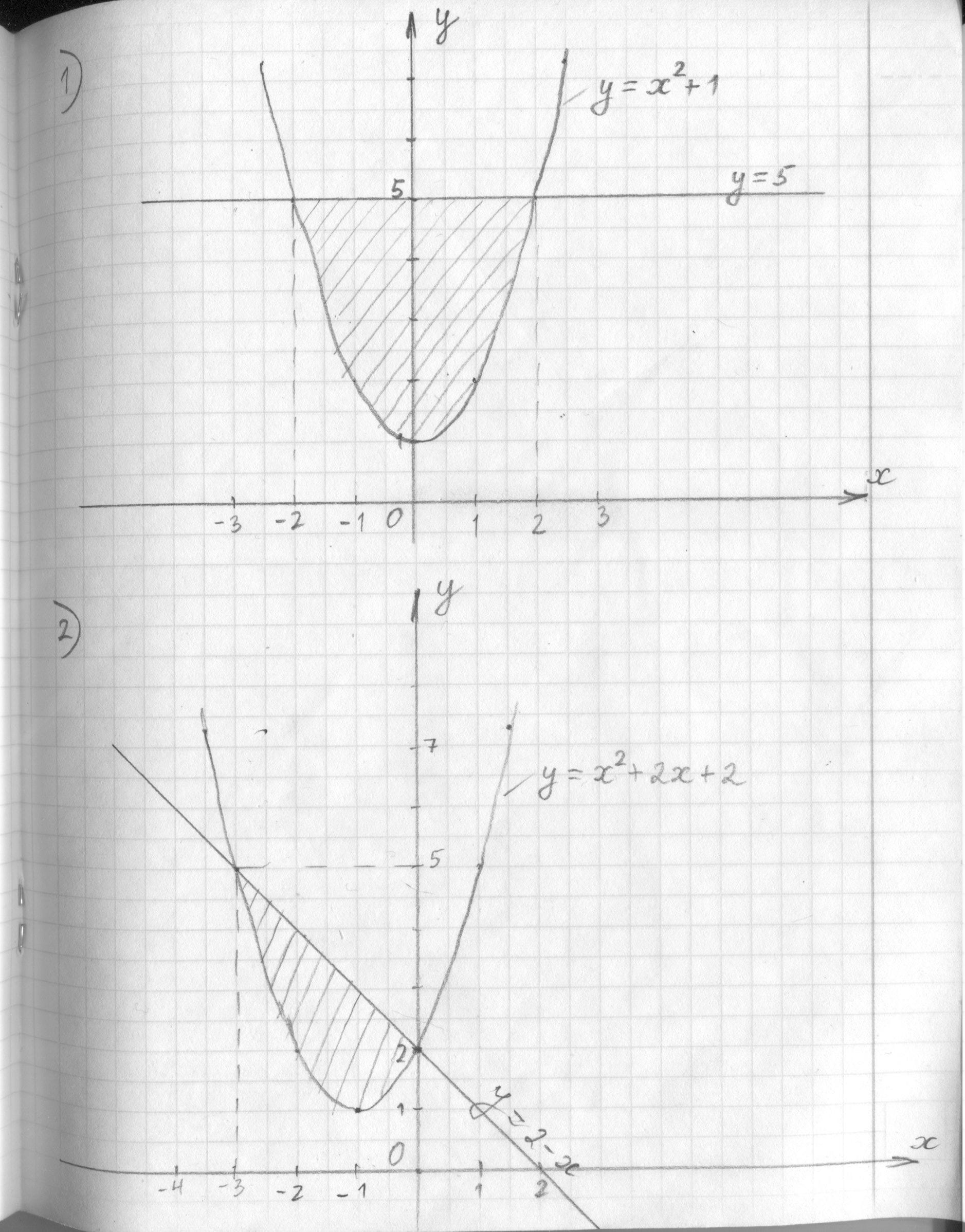
Знайти площу фігури, обмеженої графіками функцій
1)

2)

Ответы
Автор ответа:
1
1)
2)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: роза277
Предмет: Другие предметы,
автор: анита58
Предмет: Русский язык,
автор: 1325523