даны прямые a b и c известно что a параллельна b и c - секущая
определите нижеприведённые:
а) уг6=? если, уг4=50°
б)уг5=? уг7=?если, уг1=172°
в)уг8=? если,уг5-уг2=44°
г)уг3=? и уг7=? если , уг 3=5×уг7
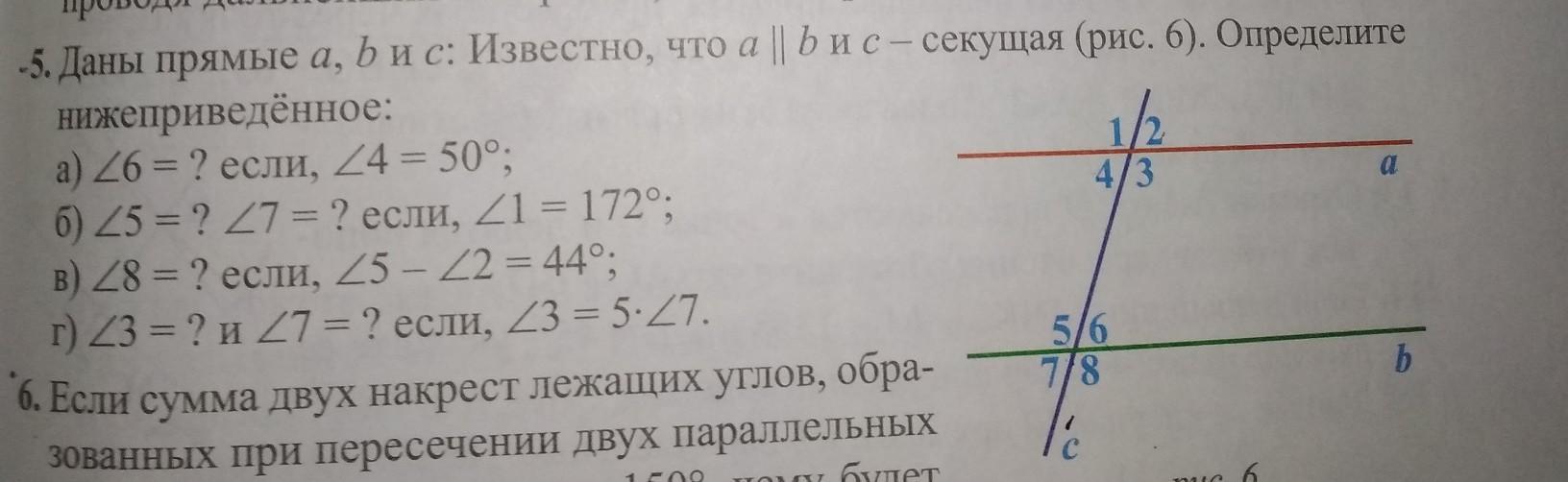
Ответы
Ответ: а) ∠6 = 50°; б) ∠5 = 172°, ∠7 = 8°; в) ∠8 = 112°; г) ∠7 = 30°, ∠3 = 150°.
Пошаговое объяснение:
Если секущая пересекает две параллельные прямые линии, то:
- внутренние накрест лежащие углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответственные углы равны;
- внешние накрест лежащие углы равны;
- сумма внешних односторонних углов равна 180°.
ДАНО:
а || b
c - секущая
РЕШЕНИЕ:
а) ∠4 = 50°, ∠6 - ?
Углы 4 и 6 - внутренние накрест лежащие углы, они равны. Значит ∠6 = ∠4 = 50°
∠6 = 50°
б) ∠1 = 172°, ∠5 - ?, ∠7 - ?
Углы 1 и 5 - соответственные углы, они равны. То есть ∠5 = 172°.
Углы 7 и 5 смежные. Сумма смежных углов равна 180°.
∠7 = 180° - ∠5 = 180° - 172° = 8°.
∠7 = 8°
в) ∠5 - ∠2 = 44°, ∠8 - ?
Поскольку углы 1 и 5 - соответственные углы, они равны. А углы 1 и 2 смежные, их сумма равна 180°. То ∠5 + ∠2 = 180°.
Выразим из этого равенства угол 2:
∠2 = 180° - ∠5
Подставим в данное выражение:
∠5 - (180° - ∠5) = 44°
∠5 - 180° + ∠5 = 44°
2 · ∠5 = 44° + 180°
2 · ∠5 = 224°
∠5 = 224° : 2
∠5 = 112°
Углы 5 и 8 - вертикальные, они равны. Значит ∠8 = 112°.
г) ∠3 = 5 · ∠7, ∠3 - ?, ∠7 - ?
Углы 3 и 6 - внутренние односторонние, углы 6 и 7 - вертикальные. Исходя из этого:
∠3 + ∠7 = 180°
Нам известно, что ∠3 = 5 · ∠7, подставим в выражение выше.
5 · ∠7 + ∠7 = 180°
6 · ∠7 = 180°
∠7 = 180° : 6
∠7 = 30°
Тогда ∠3 = 180° - ∠7 = 180° - 30° = 150°.
Углы, которые образованы при пересечении двух параллельных прямых секущей, обладают такими свойствами:
- соответственные углы равны;
- накрест лежащие углы равны;
- сумма односторонних углов равна 180°.
_________________
а) ∠6 = ∠4, как внутренние накрест лежащие углы при параллельных прямых а, b и секущей c.
Значит, ∠6 = 50°.
б) ∠5 = ∠1, как соответственные.
∠5 = 172°.
∠7 + ∠1 = 180°, так как эти углы внешние односторонние.
∠7 = 180 - 172 = 8°.
в) ∠4 = ∠2, как вертикальные.
Тогда ∠5 - ∠2 = ∠5 - ∠4 = 44°.
С другой стороны, ∠5 + ∠4 = 180°, потому что они внутренние односторонние.
Сложим почленно эти равенства:
∠5 - ∠4 + ∠5 + ∠4 = 44 + 180.
2 ⋅ ∠5 = 224
∠5 = 224 : 2
∠5 = 112°.
∠8 = ∠5, как вертикальные.
Значит, ∠8 = 112°.
г) ∠3 + ∠6 = 180°, потому что они внутренние односторонние.
∠6 = ∠7, как вертикальные.
Поэтому ∠3 + ∠7 = 180°.
По условию, ∠3 = 5 ⋅ ∠7. Подставим это выражение вместо ∠3 в верхнее равенство:
5 ⋅ ∠7 + ∠7 = 180.
6 ⋅ ∠7 = 180.
∠7 = 180 : 6
∠7 = 30°.
∠3 = 5 ⋅ 30 = 150°.
Ответ:
а) ∠6 = 50°.
б) ∠5 = 172°; ∠7 = 8°.
в) ∠8 = 112°.
г) ∠3 = 150°; ∠7 = 30°.