Question

2 1. Дана функция: у = х²– 4х + 4
а) запишите координаты вершины параболы;
b) определите, в каких четвертях находится график функции;
с) запишите ось симметрии параболы;
d) найдите точки пересечения графика с осями координат;
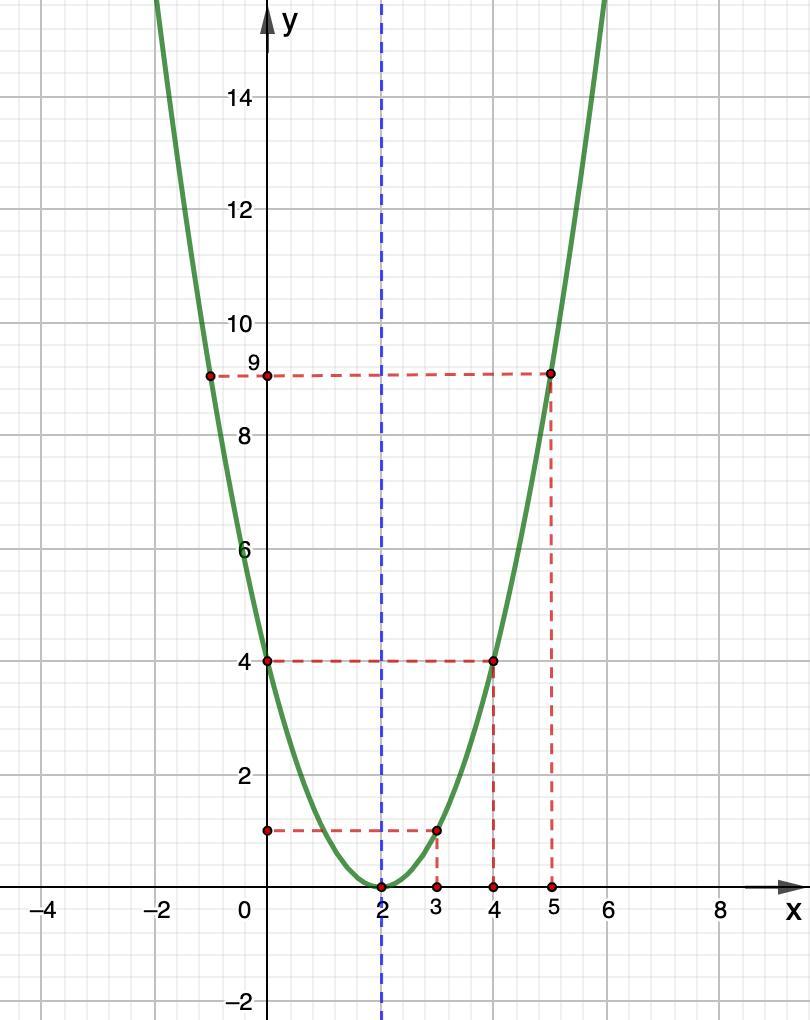
е) постройте график функции.
СРОЧНО ​

Answer 1

Ответ:

a) Координаты вершины параболы (2; 0);

b) График находится выше оси 0х, то есть в первой и второй четвертях;

с) Ось симметрии: х = 2;

d) Точки пересечения с осями координат  (0; 4);  (2; 0);

e) График построен.

Объяснение:

Требуется выполнить задание:

Дана функция: у = х²– 4х + 4

а) запишите координаты вершины параболы;

b) определите, в каких четвертях находится график функции;

с) запишите ось симметрии параболы;

d) найдите точки пересечения графика с осями координат;

е) постройте график функции.

Дана квадратичная функция вида ax² + bx + c.

у = х²– 4х + 4

- График парабола, a > 0 ⇒ ветви вверх.

a) Координаты вершины параболы:

$\displaystyle \boxed { x_0=-\frac{b}{2a} }\\\\x_0 = -\frac{-4}{2}=2\\ \\y_0=2^2-4\cdot2+4=0$

Вершина (2; 0)

b) у = х²– 4х + 4 = (х - 2)² ≥ 0

Так как y ≥ 0, график находится выше оси 0х, то есть в первой и второй четвертях.

c) Ось симметрии: х = х₀.

⇒ х = 2  - ось симметрии.

d) Точки пересечения с осями координат.

1) с осью 0у, то есть х = 0.

у = 0² - 4 · 0 + 4 = 4

⇒ точка пересечения с осью 0y имеет координаты (0; 4)

2) с осью 0х, то есть у = 0.

х² - 4х + 4 = 0

D = 4² - 4 · 4 = 0

⇒ $\displaystyle x=\frac{4\pm0}{2}=2$

⇒ точка пересечения с осью 0х имеет координаты (2; 0)

e) Дополнительные точки:

х = 3; у = 9 - 12 + 4 = 1

х = 4; у = 16 - 16 +4 = 4

х = 5; у = 25 - 20 + 4 = 9

Остальные точки строим симметрично оси симметрии х = 2.

Строим график.