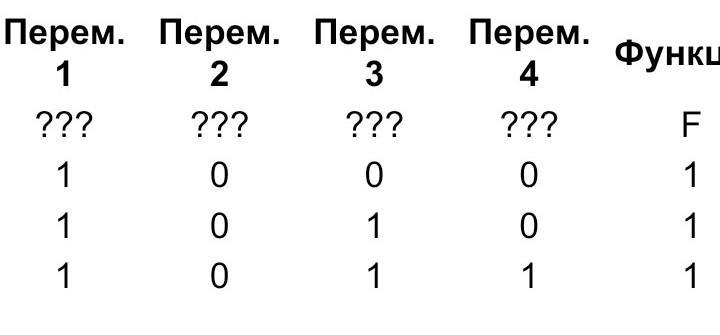
Логическая функция F задаётся выражением x ∧ ¬y ∧ (¬z ∨ w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Ответы
Ответ:
xywz
Объяснение:
выражение x ∧ ¬y ∧ (¬z ∨ w) истинно (1), когда истинны все исходные высказывания:
x - истинно
¬y - истинно
(¬z ∨ w) - истинно
переменная x в 1 столбике, т.к. всегда должна быть истинной
выражение ¬y истинно (1), когда ложно (0) исходное высказывание:
y - ложно
переменная y во 2 столбике, т.к. всегда должна быть ложной
выражение (¬z ∨ w) истинно (1), когда истинно любое из исходных высказываний:
¬z - истинно
или
w - истинно
рассмотрим 3 и 4 столбики
предположим, что в 3 столбике z, а в 4 - w
z = 0 w = 0
(¬z ∨ w) = (¬0 ∨ 0) = 1 ∨ 0 = 1 (соответствует таблице)
z = 1 w = 0
(¬z ∨ w) = (¬1 ∨ 0) = 0 ∨ 0 = 0 (не соответствует таблице)
сделаем обратное предположение (в 3 столбике w, а в 4 - z)
w = 0 z = 0
(¬z ∨ w) = (¬0 ∨ 0) = 1 ∨ 0 = 1 (соответствует таблице)
w = 1 z = 0
(¬z ∨ w) = (¬0 ∨ 1) = 1 ∨ 1 = 1 (соответствует таблице)
w = 1 z = 1
(¬z ∨ w) = (¬1 ∨ 1) = 0 ∨ 1 = 1 (соответствует таблице)
в 3 столбике w, а в 4 - z