Предмет: Геометрия,
автор: jeytaff
ПАРАЛЛЕЛЕПИПЕД - 90 БАЛЛОВ!
Дан параллелепипед ABCDA1B1C1D1
Приложения:

Ответы
Автор ответа:
3
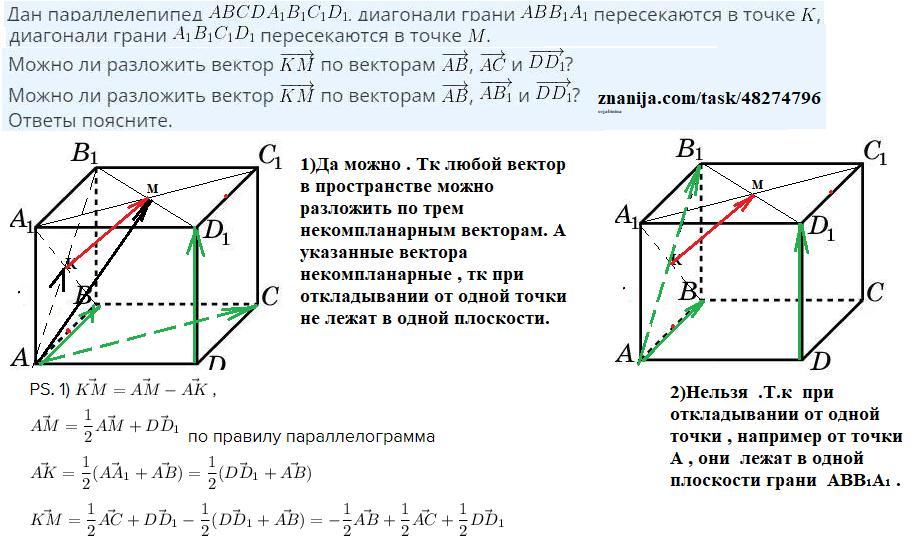
Дан параллелепипед АВСDA₁B₁C₁D₁ . Диагонали грани АВВ₁А₁ пересекаются в точке К . Диагонали грани А₁В₁С₁D₁ пересекаются в точке М.
1)Можно ли разложить вектор КМ по векторам АВ, АС, DD₁ ?
2)Можно ли разложить вектор КМ по векторам АВ, АВ₁, DD₁ ?
Решение
1)Да можно . Тк любой вектор в пространстве можно разложить по трем некомпланарным векторам. А указанные вектора некомпланарные , тк при откладывании от одной точки не лежат в одной плоскости.
2)Нельзя .Т.к при откладывании от одной точки , например от точки А , они лежат в одной плоскости грани АВВ₁А₁ .
=======================================
PS. 1) ,
по правилу параллелограмма
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: братства
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: lapschinalexej
Предмет: Математика,
автор: wwwanku