Question

Помогите пожалуйста решить

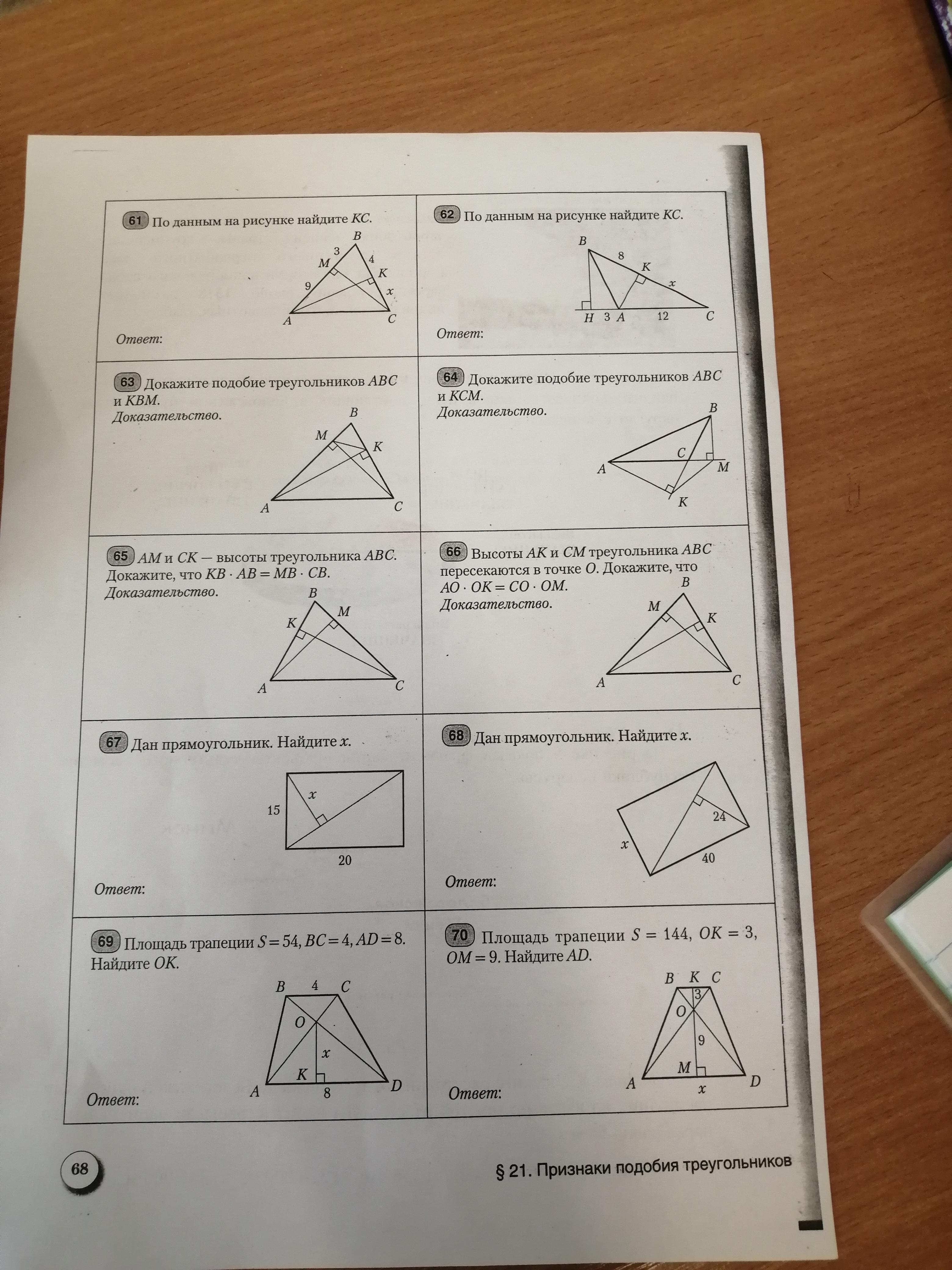
Задача номер 69

ABCD - Трапеция, BC=4см, AD=8см, S(abcd)=54см^2
OK-?

Answer 1

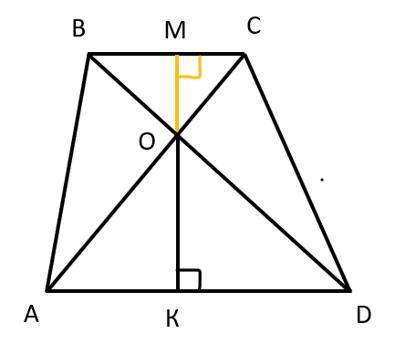
Продлим перпендикуляр ОК до пересечения с верхним основанием трапеции.

Получаем высоту трапеции МК.

Формула площади трапеции:

$S = \frac{a+b}{2} \cdot h$, где а, b — основания, h — высота.

Подставим в формулу данные из задачи и решим полученное уравнение:

$\frac{4+8}{2} \cdot MK = 54$

$6 \cdot MK = 54$

$MK = 54 : 6$

$MK = 9$.

∠BOC = ∠AOD, как вертикальные углы.

Поскольку ABCD — трапеция, то BC║AD.

∠CBO = ∠ODA, как внутренние накрест лежащие при параллельных прямых BC и AD и секущей BD.

Значит, ΔOBC ~ ΔOAD по двум углам.

У подобных треугольников длины соответствующих элементов пропорциональны.

Значит, $\frac{OK}{OM} =\frac{BC}{AD}$.

$\frac{OK}{OM}=\frac{8}{4}=2 .$

Тогда получается, что ОК больше, чем ОМ в 2 раза. Поэтому, если ОК обозначить как х, то ОМ равно $0,5x$.

Вместе ОК и ОМ образуют высоту трапеции, длину которой мы уже вычислили выше. Теперь можем составить и решить уравнение:

$0,5x +x = 9$

$1,5x = 9$

$x = 9 : 1,5$

$x = 6$.

Ответ: ОК = 6 см.