найдите медианы треугольника со сторонами 13,13 и 10 см СРОЧНО ПОЖАЛУЙСТА ДАМ 100 БАЛЛОВ!!!
Ответы
Ответ:
Медианы треугольника пересекаютя и точка персечения делит медиану в соотношении 2:1. пусть а и в-стороны=13, с=10, тогда медиана опущенная на сторону а равна м=1/2√(2в² 2с²-а²) подставляем м=1/2√(2*13² 2*10²-13²)=1/2√338 200-169)=1/2√369=3/2*√41
м=1/2√(2в² 2с²-а²)-это формула вычисления медианы через стороны треугольника.
так как треуг равнобедренн, то и медианы опущенные на стороны а и в равны.
Пошаговое объяснение:
Ответ:
Пошаговое объяснение:
для вычисления длины медианы треугольника используем формулы
Ma=1/2*√(2b² + 2с²- а²) - медиана, проведенная к стороне а
Mb=1/2*√(2a² + 2с²- b²) - медиана, проведенная к стороне b
Mc=1/2*√(2a² + 2b²- c²) - медиана, проведенная к стороне c
подставляем
пусть а=13 b=13 c=10
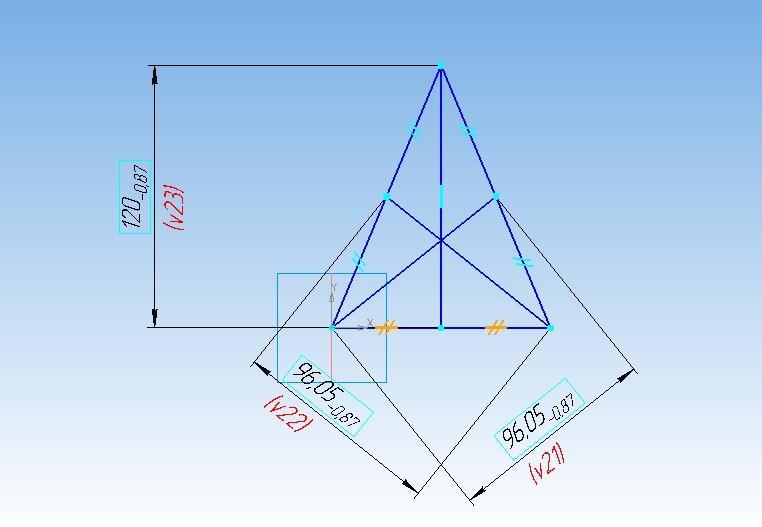
Ma=1/2*√(2b² + 2с²- а²) = 1/2*√(2*13² + 2*10²- 13²) = 3/2*√41 ≈ 9,6047 см - это ответ
Mb=1/2*√(2a² + 2с²- b²) = 1/2*√(2*13² + 2*10²- 13²) = 3/2*√41 ≈ 9,6047 см - это ответ
Mc=1/2*√(2a² + 2b²- c²) = 1/2*√(2*13² + 2*13²- 10²) = 12 см - это ответ
как видим две медианы равны между собой (так как треугольник равнобедренный)
а третья отличается
на скриншоте размеры в мм отличаются в 10 раз
https://znanija.com/task/48647835
https://znanija.com/task/48647836
https://znanija.com/task/48647841
https://znanija.com/task/48647845