Предмет: Алгебра,
автор: sofiamyasnikova03
вычислить средне арифметическое корней уравнения
Приложения:
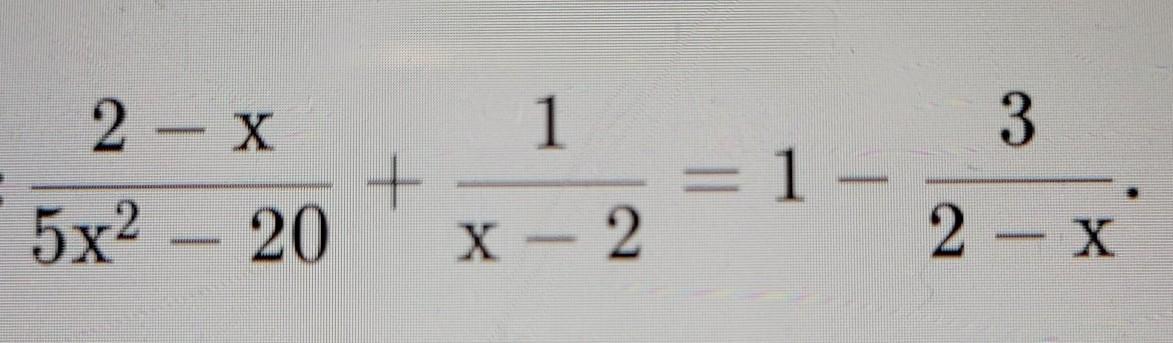
Ответы
Автор ответа:
1
ОДЗ: 5x² - 20 ≠ 0 и x-2 ≠ 0,
x² - 4 ≠ 0
x ≠ 2 и x≠ -2.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: lola158
Предмет: Английский язык,
автор: alla510
Предмет: Физика,
автор: Николь123451257875
Предмет: Қазақ тiлi,
автор: siiii18