катушка с нитью общей массой 19г находится на наклонной плоскости с углом наклона 30 градусов. Для удержания катушки в состоянии покоя к свободному концу нити приложили силу F, параллельно наклонной плоскости. Если диаметр катушки D=6 см, а радиус намотки нити r=2см, то модуль силы F равен... H×m

Ответы
Ответ:
- F=57 мН
Объяснение:
Дано:
m=19г=0,019 кг
D=6см=0,06 м
r=2см=0,02 м
α=30°
g=10 Н/кг
Найти: F-?
Решение:
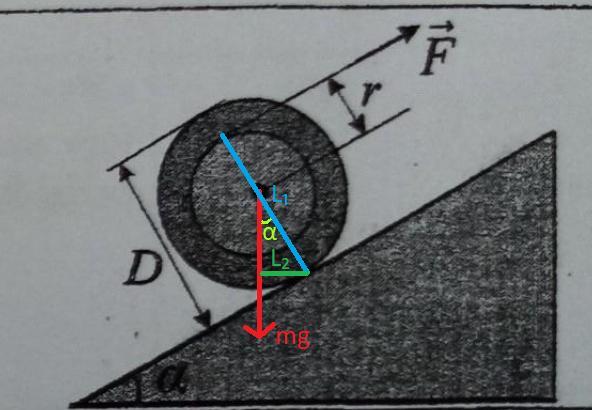
За ось вращения примем точку соприкосновения катушки с плоскостью, тогда моментом силы трения и реакции опоры можно пренебречь, т.к. они проходят через ось вращения.
Тогда примем во внимание только силу тяжести и приложенную силу F.
Чтобы катушка была в состоянии покоя, моменты М₁ и М₂ сил F и соответственно должны быть равны, то есть M₁=M₂ ⇔
, где
,
.
Тогда
Відповідь:
Mодуль силы F равен 56 мН.
Пояснення:
Если тело находится в равновесии ( в состоянии покоя ) , то это значит, что сумма приложенных к нему сил равна нулю и сумма моментов этих сил относительно оси , вокруг которой тело может вращаться, также равна нулю.
Момент силы — это произведение силы на плечо:
M = Fl , где
M — момент силы [Н·м]
F — сила [Н]
l — плечо [м].
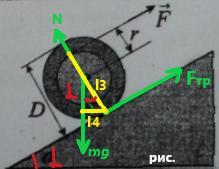
Поэтому, М₁+М₂+М₃+М₄=0,
где М₁= N·l₁= N·0=0,
M₂=Fтр·l₂=Fтр·0=0,
M₃=F·l₃,
M₄= - mg·l₄.
Итак, F·l₃ - mg·l₄=0,
F·l₃= mg·l₄.
Найдём плечи l₃ и l₄.
Плечо приложенной силы F равно :
l₃= D/2+r.
Плечо силы тяжести Fт равно :
l₄= D/2·sinα = D/2·sin30⁰( смотреть рис.)
Итак,
F=(mg·l₄)/l₃= (mg·D/2·sin30⁰)/(D/2+r) = (0,019 ·9,8·0,06/2·0,5)/(0,06/2+0,02)= 0,002793/0,05=0,05586 H ≈ 0,056H = 56 мН .