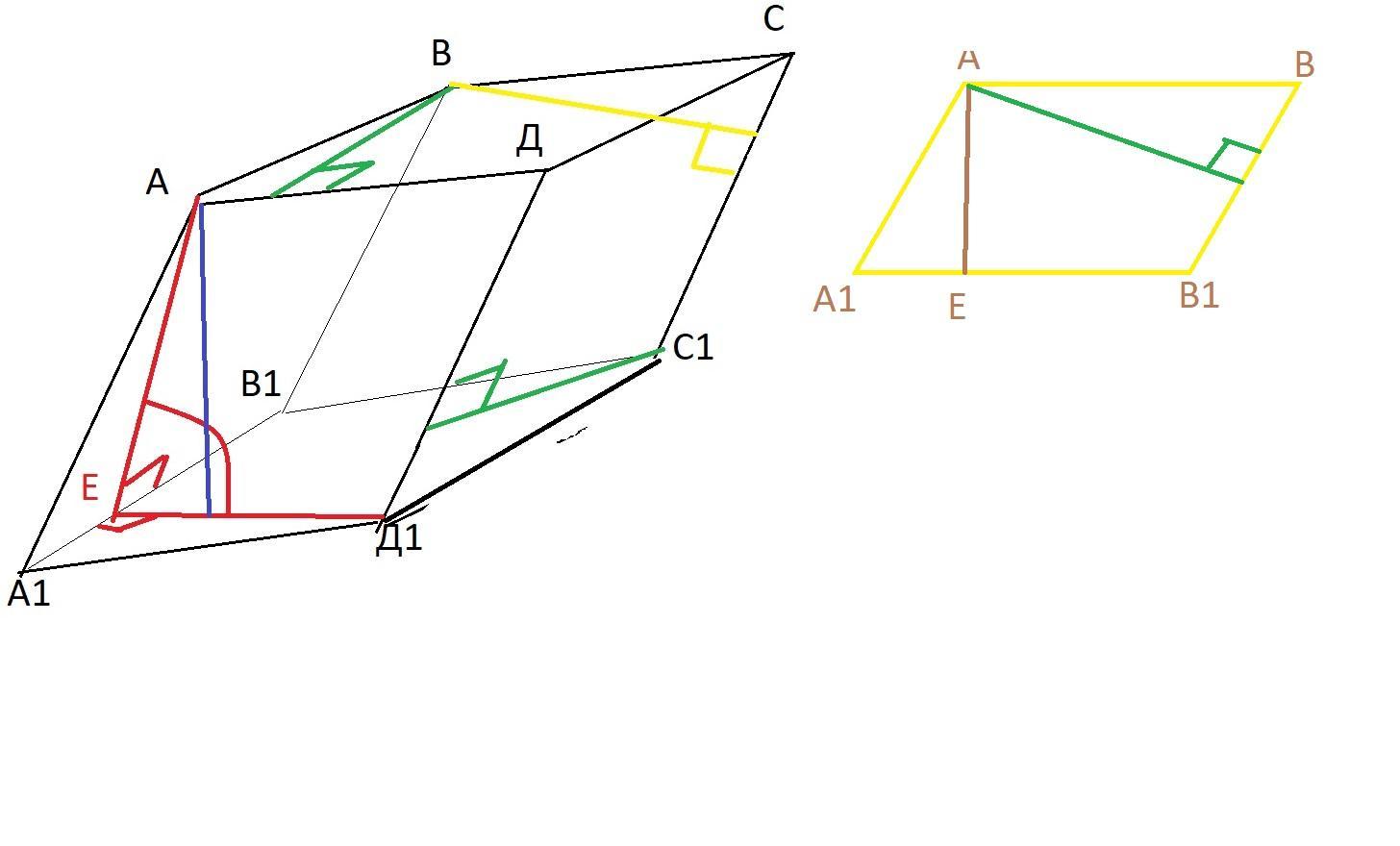
Боковое ребро наклонного параллелепипеда ABCDA1B1C1D1 равно 8 см. Расстояние между прямыми AA1 и BB1 равно 2 см между прямыми BB1 и CC1 - 3 см а двугранный угол параллелепипеда при ребре BB1 равен 45. Найдите объём параллелепипеда
С рисунком
Ответы
Ответ:
Объяснение:
Vплп= h*Sосн
каждая сторона параллелепипеда это параллелограмм.
Боковое ребро АА1=ВВ1=СС1=ДД1=8
∠АЕД1 =45 двугранный угол параллелепипеда при ребре BB1
Sосн= 2*3
h= 8*sin45=4√2
V = 6*4√2 = 24√2
Боковое ребро наклонного параллелепипеда ABCDA₁B₁C₁D₁ равно 8 см. Расстояние между прямыми AA₁ и BB₁ равно 2 см , между прямыми BB₁ и CC₁- 3 см , а двугранный угол параллелепипеда при ребре BB₁ равен 45°. Найдите объём параллелепипеда.
Решение.
Т.к. наклонный параллелепипед это наклонная призма , то обьем можно найти по теореме " Объем наклонной призмы равен произведению бокового ребра на площадь сечения призмы плоскостью, перпендикулярной к боковым ребрам и пересекающей их" .
Пусть А₁К⊥ВВ₁ и МК⊥ВВ₁. Используя параллельность противоположных граней получаем , что плоскость (А₁КМ)⊥ВВ₁ и А₁КМР-параллелограмм.
Линейным углом двугранного угла АВВ₁С будет ∠А₁КМ=45° , т.к. А₁К⊥ВВ₁ и МК⊥ВВ₁.
S( параллелограмма А₁КМР)=А₁К*КМ*sin(∠А₁КМ),
S( параллелограмма А₁КМР)=2*3*sin 45°=3√2 (см²).
V(наклонного параллелепипеда)=8*3√2=24√2 (см³).
