Предмет: Геометрия,
автор: muminovam587
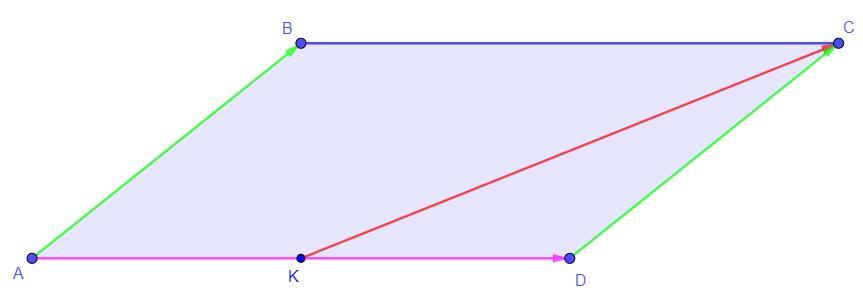
2. Точка K — середина стороны AD параллелограмма ABCD. Выразите вектор КС через векторы AB и AD. Пожалуйста помогите
Ответы
Автор ответа:
4
Ответ:
Объяснение:
Так как точка K— середина стороны AD по условию, то , следовательно вектор
. Так как
и точка середина K есть середина отрезка, то
.
Так как по свойствам параллелограмма его противоположные стороны равны и параллельны, то вектор .
По правилу треугольника:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: salkimbaeva18
Предмет: Русский язык,
автор: Avon1986
Предмет: Другие предметы,
автор: Аликона
Предмет: Русский язык,
автор: 1337reykin
Предмет: Математика,
автор: aidol81