Предмет: Физика,
автор: shymka102ry
Кто знает как решить? Тема кинематика материальной точки
Приложения:
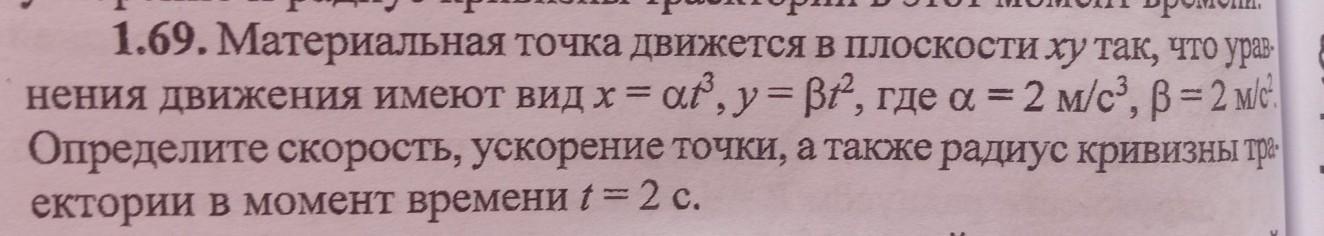
Ответы
Автор ответа:
1
Ответ:
v₁ ≈ 25.30 м/с; a₁ ≈ 24,33 м/с²; ρ₁ ≈ 168,65 м.
Объяснение:
x(t) = 2t³
y(t) = 2t²
t₁ = 2c
------------------
v₁ , a₁, ρ₁ - ?
-----------------
Проекции скорости
При t₁ = 2c
Скорость
Проекции ускорения
При t₁ = 2c
Ускорение
Тангенциальное ускорение
Нормальное ускорение
Радиус кривизны
shymka102ry:
спасибо большое
Похожие вопросы
Предмет: Английский язык,
автор: Katya071111
Предмет: Русский язык,
автор: Łųçů
Предмет: Русский язык,
автор: 19572006
Предмет: Русский язык,
автор: RAMILRAMA