Предмет: Алгебра,
автор: rtrukpenov5
ПОЖАЛУЙСТА РЕШЕТИИИИ
Приложения:
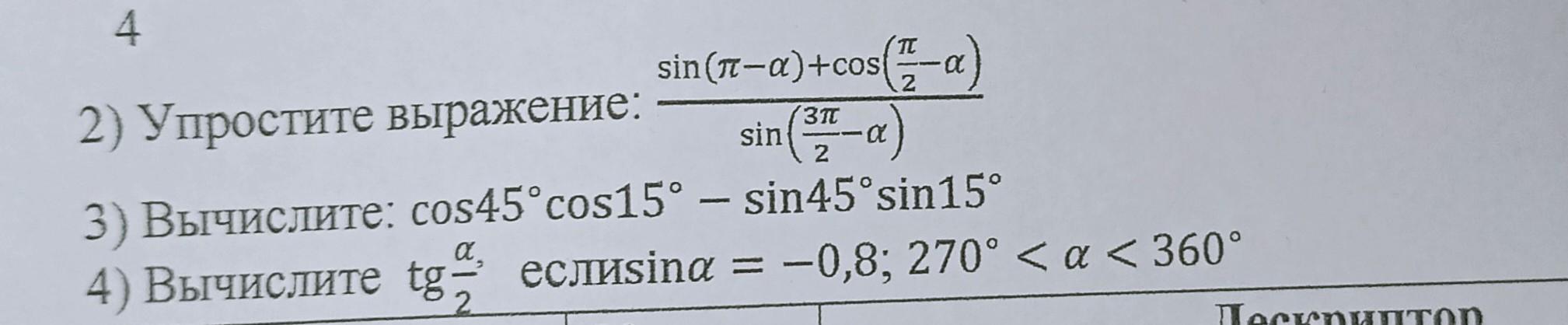
Ответы
Автор ответа:
1
Ответ:
Применили формулы приведения.
Формула косинуса суммы.
или
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: зарифа8
Предмет: Другие предметы,
автор: настя20051607
Предмет: Другие предметы,
автор: fisher78
Предмет: Математика,
автор: nxjjsjsjs
Предмет: Французский язык,
автор: vassilisapnmareva