Question

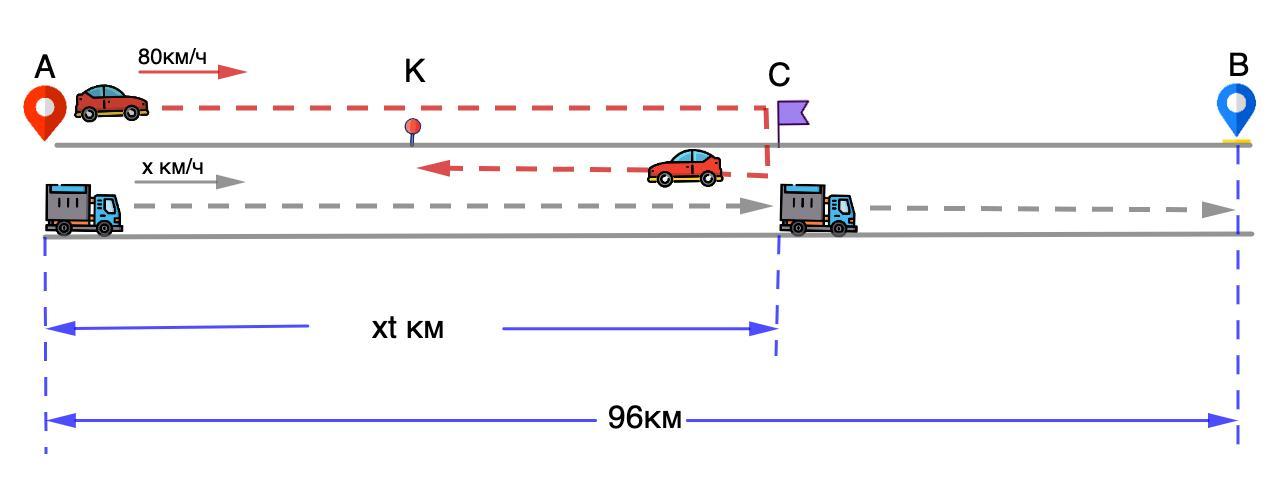
Между пунктами А и Б расстояние в 96 км. Из пункта А по направлению в пункт Б направился грузовик, спустя 90 минут за ним отправился легковой автомобиль со скоростью 80 км/ч. Автомобиль достиг грузовик в пункте С, потом развернулся и поехал обратно. Когда грузовик доехал до пункта Б, то автомобиль проехал половину пути от пункта С до А. Найдите, сколько км составляет расстояние от пункта А до С.
СРОЧНОО

Answer 1

Ответ:

Расстояние от пункта А до С равно 80 км.

Пошаговое объяснение:

Найти, сколько км составляет расстояние от пункта А до С.

Вспомним формулы:

$\displaystyle \boxed {S=vt}\;\;\;\;\;\boxed {t=\frac{S}{v} }\;\;\;\;\;\boxed {v=\frac{S}{t} }$

1. Пусть скорость грузовика х км/ч, а время, за которое грузовик доехал до пункта С - t ч.

Скорость автомобиля - 80 км/ч.

90 мин. = 1,5 ч.

Так как автомобиль выехал на 1,5 ч позже, то время, за которое автомобиль доехал до пункта С, равно (t - 1,5) ч.

Так как грузовик и автомобиль проехали одинаковое расстояние АС, то это расстояние равно:

АС = xt (км) или АС = 80(t - 1,5) км

Составим уравнение и выразим х:

$\displaystyle xt=80(t-1,5)\\\\xt=80t-120\\\\\boxed {x=\frac{80t-120}{t} }$             (1)

2. Рассмотрим движение от пункта С.

Автомобиль развернулся и доехал до отметки К, что составляет половину АС.

Если расстояние АС автомобиль проехал за (t - 1,5) ч, то половину этого расстояния он проедет за

$\displaystyle \frac{t-1,5}{2}$  ч.

Грузовик за это время проехал расстояние СВ:

СВ = 96 - АС = (96 - xt) (км)

Скорость грузовика х км/ч, можем выразить время:

$\displaystyle \frac{96-xt}{x}$  ч.

Время, за которое автомобиль проехал расстояние СК равно времени грузовика, за которое грузовик проехал расстояние СВ.

Составим уравнение:

$\displaystyle \frac{t-1,5}{2}=\frac{96-xt}{x}\;\;\;|\cdot2x,\;x\neq 0\\\\xt-1,5x=192-2xt\\\\3xt-1,5x-192=0$

Подставим вместо х его выражение (1):

$\displaystyle 3t\cdot\frac{80t-120}{t}-1,5\cdot\frac{80t-120}{t}-192=0\;\;\;|\cdot{t},\;t\neq 0\\\\240t^2-360t-120t+180-192t=0\\\\240t^2-672t+180=0\;\;\;|:4\\\\60t^2-168t+45=0\\\\t_{1,2}=\frac{168\pm\sqrt{28224-10800} }{120}=\frac{168\pm132}{120}\\ \\ t_1=2,5;\;\;\;\;\;t_2=0,3$

t₂ = 0,3 - не подходит, так как по условию t > 1,5 ч.

⇒ t = 2,5 ч.

Можем найти АС:

АС = 80 (t - 1,5) = 80(2,5 - 1,5) = 80 (км)

Расстояние от пункта А до С равно 80 км.