Предмет: Алгебра,
автор: nastasya0410
помогите1 вариант очень нужно ...
Приложения:

Ответы
Автор ответа:
0
1. при х от  до 1 - у увеличивается быстро, после чего практически не увеличивается
до 1 - у увеличивается быстро, после чего практически не увеличивается
2. a)
б)
3.
однако, под логарифмом не может быть отрицательное число, поэтому накладывается условие
объединив эти 2 решения, получаем, что
4.
корень х=-4 не подходит, т.к. по свойству логарифма х>0
Ответ:
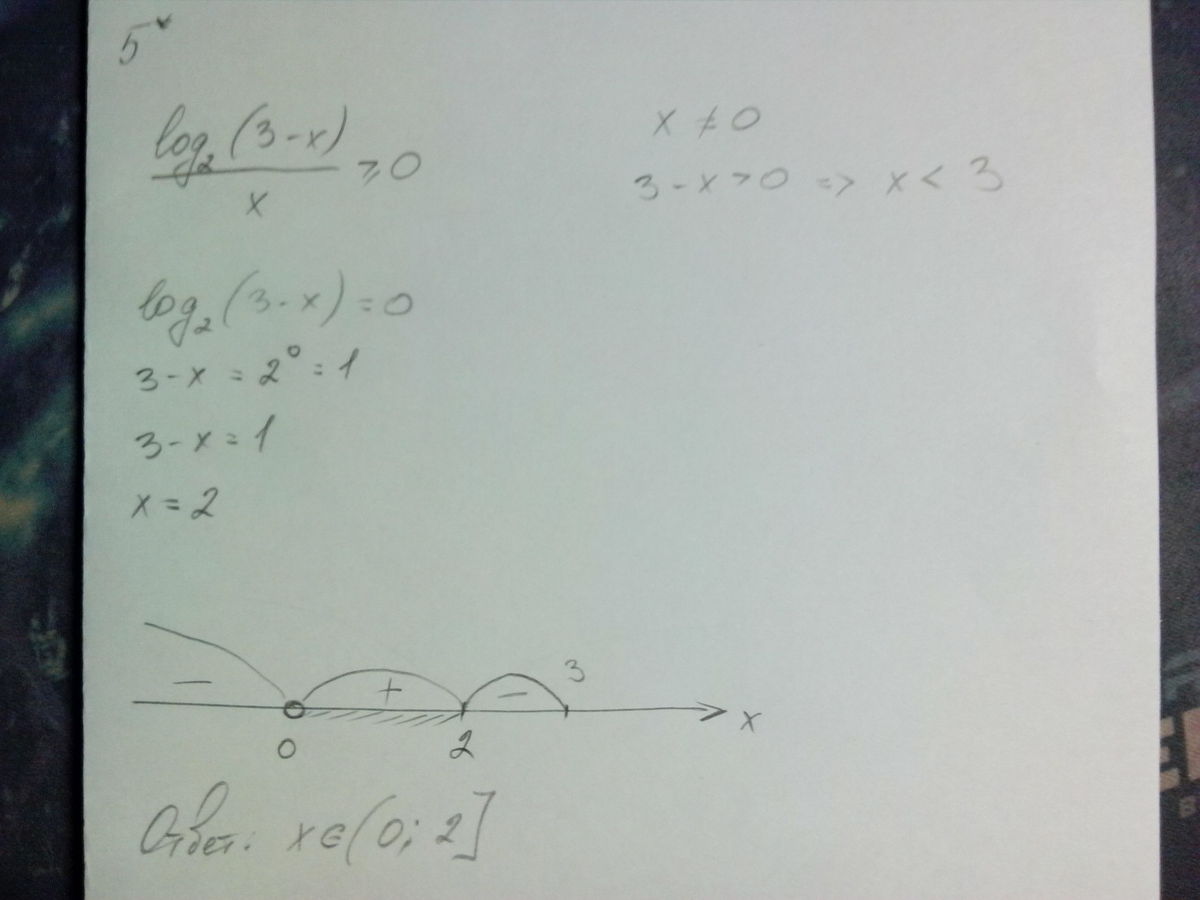
5* решение на фотке
2. a)
б)
3.
однако, под логарифмом не может быть отрицательное число, поэтому накладывается условие
объединив эти 2 решения, получаем, что
4.
корень х=-4 не подходит, т.к. по свойству логарифма х>0
Ответ:
5* решение на фотке
Приложения:

Автор ответа:
0
отредактировал, пардоньте, не заметил
Автор ответа:
0
я апрям благодарна тебе добрый человек, дай бог тебе здоровья!!!:))))))
Автор ответа:
0
так уж и быть, можешь лучшего поставить :D
Автор ответа:
0
а это как
Автор ответа:
0
а не знаю, как то ставят лучший ответ, я хз, не задавал вопросы :D
Похожие вопросы
Предмет: Математика,
автор: adukiko
Предмет: Литература,
автор: nikita07pasik
Предмет: Физика,
автор: proverkaqwe123
Предмет: Информатика,
автор: Этанол