Question

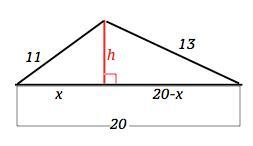
знайдіть найменшу высоту трикутника зі сторонами 11, 20, 13​

Answer 1

Ответ:

6.6

Нужно 2 вещи.

1) Формула Герона

2) Формула площади по стороне и высоте, на нее опущенной.

S= $\sqrt{p*(p-a)*(p-b)*(p-c)}$

S=ah/2 - заметим сразу, что наименьшая высота будет у наибольшей стороны.

h=2 $\sqrt{p*(p-a)*(p-b)*(p-c)}$/a

p=(a+b+c)/2

_____________

Решаем.

p=(11+20+13)/2=44/2=22

h=2($\sqrt{22(22-11)(22-20)(22-13)}$/20≈66/10=6.6

Ищу лучший ответ.

 

Answer 2

Ответ: 6,6

Вариант решения.

 Формула площади треугольника S=a•h/2 => h=2S:a.=>

 Чем больше сторона треугольника, тем меньше высота, которая к ней проведена.

   Пусть высота, проведенная к стороне 20, делит ее на отрезки х и 20-х, и образует два прямоугольных треугольника, гипотенузы которых - другие стороны исходного треугольника.

 Выразим квадрат высоты из 1-го треугольника по т.Пифагора:

h²= 11²-х²

Аналогично – то же  из второго треугольника:

h²=13²-(20-x)²

Приравняем эти значения

11²-х²=13²-(20-x)² Решив уравнение, получим

40х=352

х=8,8

Из меньшего треугольника по т.Пифагора

h=√(121-77,4)= 6,6 ( ед. длины)