Предмет: Алгебра,
автор: fox221021
Решите пожалуйста неравенства
Приложения:
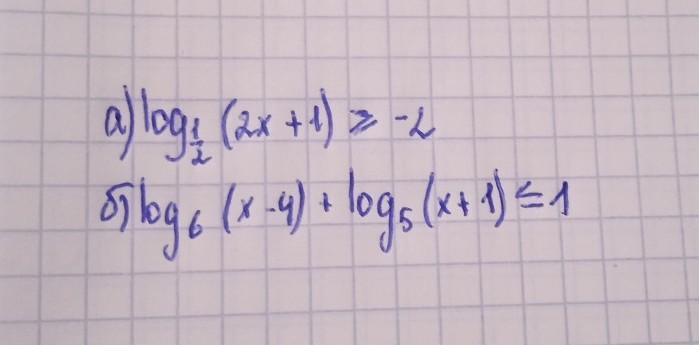
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1) log₁₎₂(2x+1)≥-2
ОДЗ: 2х+1>0 ⇒ x> - 0,5, т.е. x∈(-0,5; +∞)
преобразуем уравнение: log₁₎₂(2x+1) ≥ log₁₎₂ 4
основание логарифма 0 <1/2 <1 , значит функция у=log₁₎₂(2x+1) убывающая ⇒
2х+1 ≤ 4
2x≤3
x≤1,5 сравним полученное решение с ОДЗ, тогда имеем, что
х∈ (-0,5 ; 1,5]
Ответ: (-0,5 ; 1,5]
2) log₆ (x-4) + log₆(x+1)≤1
ОДЗ: x-4>0 b и x+1>0 ⇒ x>4
log₆ (x-4)(x+1)≤ log₆ 6
log₆ ( основание 6>1 функция возрастающая⇒x²-3x-4≤ 6
x²-3x-4 -6≤ 0
x²-3x - 10 ≤ 0
D=49
x₁=5 x₂ =-2 ⇒x∈(-∞;-2)∪(5;+∞)
сравним полученное решение с ОДЗ, тогда имеем, что
х∈ (5;+∞)
Похожие вопросы
Предмет: Английский язык,
автор: lera2114
Предмет: Окружающий мир,
автор: юмилана
Предмет: Русский язык,
автор: алеся90
Предмет: Английский язык,
автор: gvikaa
Предмет: Физика,
автор: Efimovaas05