Предмет: Математика,
автор: 1cshrbn91lf3ybbk
сколько целочисленных решений имеет неравенство?

Ответы
Автор ответа:
1
далее решим уравнение
2x²-3x-2=0
D= (-3)²-4•2•(-2)=25
поэтому наше неравенство можно переписать
2(x-2)(x+½)≤0
(x-2)(x+½)≤0
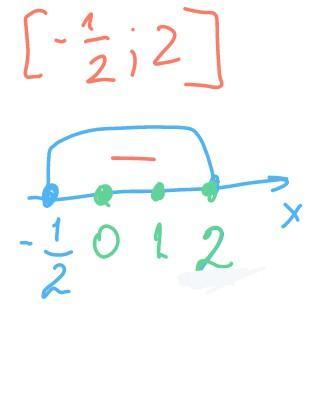
решим методом интервалов (см рисунок)
как видим, решением неравенства будет
х€ [ -½ ; 2]
о целочисленных решений, попавших в этот интервал, будет 3
х€ { 0, 1, 2 }
Ответ: 3
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: дарья1115
Предмет: Русский язык,
автор: Дарья11211167
Предмет: Английский язык,
автор: sheldayka