Предмет: Математика,
автор: Lalatina31
Дана кривая 2-ого порядка. Привести ее к каноническому виду и показать, что это окружность. Найти ее радиус, центр и построить:
Приложения:
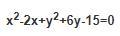
Ответы
Автор ответа:
1
Ответ:
A(1; -3), r=5
Пошаговое объяснение:
уравнение окружности с центром в точке А(х0;у0) и радиусом r
выделим полные квадраты при переменных х и у:
- окружность с центром в точке А(1; -3) и радиусом r=5
Похожие вопросы
Предмет: Русский язык,
автор: Dimos457
Предмет: Английский язык,
автор: тЕМ2015
Предмет: Английский язык,
автор: OkaRuto
Предмет: Математика,
автор: Katay201819
Предмет: Химия,
автор: choser