Предмет: Математика,
автор: danil31r121
Объясните противоречие. Если k брать как тангенс, то k=0,4, а если решать системой то k=-0,4. Почему?
Приложения:
Ответы
Автор ответа:
2
Пошаговое объяснение:
Дело в том, что по свойствам модуля
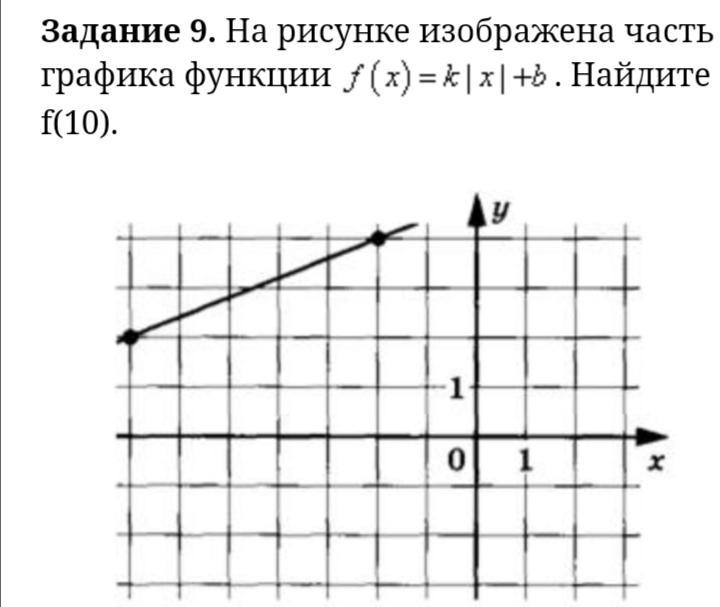
На рис. показана часть графика, в которой
х < 0
=> для данного участка справедливо:
В нашем случае, при возрастании х в отрицательных значениях значения (-х) убывают.
Однако мы видим, что при возрастании значений х (в отрицательном секторе) значение функции возрастает, а следовательно, значение
-kx > 0 => k < 0
Короче, при х < 0 мы "имеем дело" с "-х", а значит перед kx стоит знак минус, который и нужно учесть при графической интерпретации рисунка
Похожие вопросы
Предмет: Английский язык,
автор: спасибкивсем
Предмет: Русский язык,
автор: alecy3179
Предмет: Английский язык,
автор: Славка25
Предмет: Русский язык,
автор: zahoruikoo
Предмет: Русский язык,
автор: eldarboronaj