Question

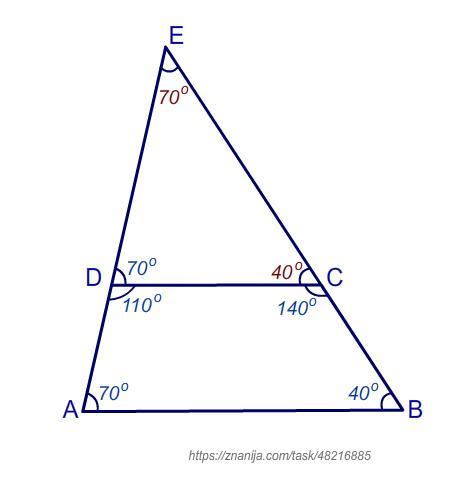
У трапеції АВСD AB-більша основа. Прямі BC i AD перетинаються в точці E.
Кут ECD=40° кут BEA=70° Знайдіть кути трапеції

Answer 1

Ответ:

В трапеции ABCD

∠ABC = 40°;

∠DCB = 140°;

∠ADC  = 110°;

∠DAB  = 70°.

Пошаговое объяснение:

Найти углы трапеции по данным задачи.

Дано:
ABCD - трапеция, AB - большее основание, прямые BC и AD пересекаются в точке Е;  ∠ECD = 40° ∠BEA=70°.

Найти: углы трапеции ∠ABC, ∠DCB, ∠ADC, ∠DAB.

Решение.

• Трапеция - это четырехугольник, у которого две стороны параллельны (основания), а две другие не параллельны (боковые стороны).

1) В трапеции ABCD основания AB ║CD.

По условию ∠ECD = 40°.

∠ECD = ∠ABE как соответственные углы при AB ║CD и секущей BE.

⇒ ∠ABE = 40°.
В трапеции ∠ABC = 40°.

• Сумма смежных углов равна 180°.

2) ∠ECD и ∠DCB смежные углы (две стороны EC и CB этих углов являются дополнительными полупрямыми, и одна сторона CD общая).

∠ECD + ∠DCB = 180°;

∠DCB = 180° - ∠ECD = 180° - 40° = 140°.

В трапеции ∠DCB = 140°.

• Сумма углов треугольника равна 180°.

3) В ΔDEC известны два угла. Найдем ∠EDC.

∠EDC = 180° - ∠DEC - ∠ECD = 180° - 70° - 40° = 70°.

∠EDC = 70°.

4) ∠EDC и ∠ADC смежные углы.

∠ADC = 180° - ∠EDC = 180° - 70° = 110°.

В трапеции ∠ADC  = 110°.

5) ∠EDC и ∠DAB соответственные углы при параллельных прямых AB ║CD и секущей AE.

∠EDC = ∠DAB = 70°.

В трапеции ∠DAB  = 70°.