Question

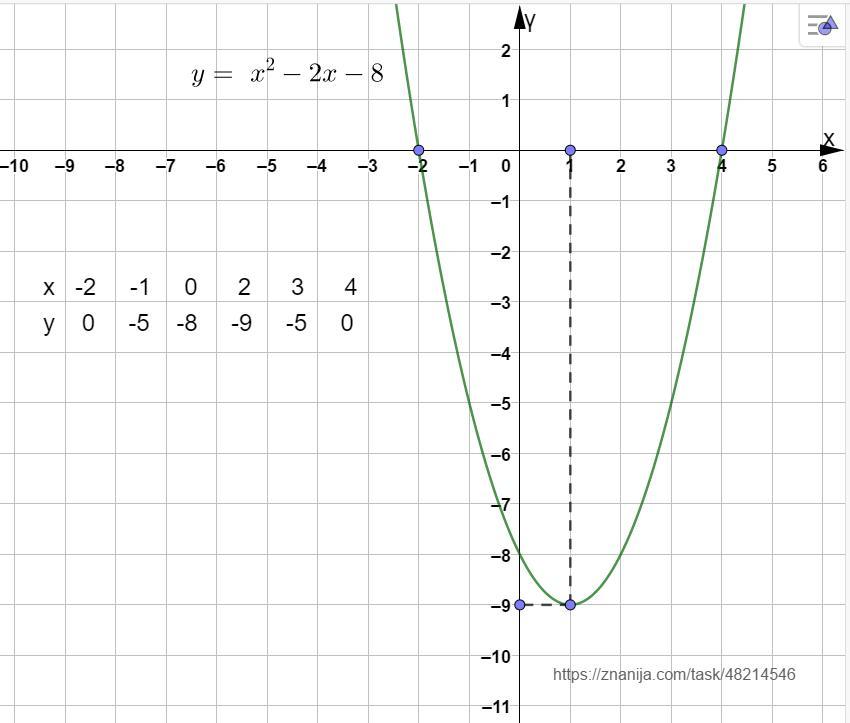
Найдите на какую максимальную глубину ныряют дельфины .если уравнение движения имеет вид у=x^2-2x -8 Постройте график данной функции.​

Answer 1

Ответ:

Дельфин ныряет на максимальную глубину 9 м.

Объяснение:

Определить максимальную глубину, на которую ныряют дельфины, по заданному уравнению движения:

y = x² - 2x - 8.

Построить график данной функции.

• Функция вида  f(x) = ax² + bx + c  - это квадратичная функция, ее графиком является парабола.

Уравнение движения дельфина y = x² - 2x - 8 является квадратичной функцией. Построим график функции.

1) Областью определения заданной функции является множество всех чисел.

D(y) = R.

2) Графиком данной квадратичной функции  y = x² - 2x - 8 является парабола.

Старший коэффициент a = 1,  a > 0. Ветви параболы направлены вверх.

3) Вершина параболы:

$\displaystyle x_{0} = \frac {-b}{2a};\\\\\\x_{0} = \frac {-2}{2} =1.$

Прямая x = 1 является осью симметрии параболы.

y₀ = 1² - 2 · 1 - 8 =-9

Вершина параболы находится в точке (1; -9).

• Нули функции - это значения аргумента, при которых функция равна нулю: f(x) = 0. В этих точках график функции пересекает ось OX.

4) Нули функции (точки пересечения оси OX).

y = 0;

x² - 2x - 8 = 0;

D = b² - 4ac = 2² - 4 · 1 · (-8) = 4 + 32 = 36 = 6².

$\displaystyle x_{1,2} =\frac{-b\pm\sqrt{D} }{2a};$

$\displaystyle x_{1} =\frac{-b-\sqrt{D} }{2a} = \frac{2-6}{2} = -2\\\\\\x_{2} =\frac{-b+\sqrt{D} }{2a} = \frac{2+6}{2} = 4.$

График функции пересекает ось OX в точках x = -2 и x = 4.

5) Пересечение оси OY.

• График функции пересекает ось OY при условии x = 0.

При x = 0 значение y = -8.

6) Составим таблицу значений аргументов и значений функции (в приложении).

x = -2,  y  = 0;

x = -1,  y  = (-1)² - 2·(-1) -8 = 1 + 2 - 8 = -5;

x = 0,  y  = -8;

x = 1,  y  = -9;

x = 2,  y = -8.

x = 3,  y  = -5;

x = 4,  y  = -0;

7) Построим график функции. График прилагается.

8) Наибольшая глубина погружения дельфина соответствует наименьшему значению функции.

Наименьшее значение функции соответствует вершине параболы:
y = -9.

Дельфин ныряет на максимальную глубину 9 м.